2005 AMC 12A Problems/Problem 7
Contents
Problem
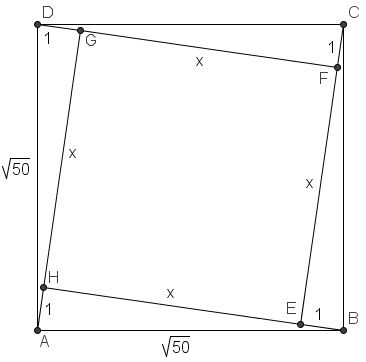
Square ![]() is inside the square
is inside the square ![]() so that each side of
so that each side of ![]() can be extended to pass through a vertex of
can be extended to pass through a vertex of ![]() . Square
. Square ![]() has side length
has side length ![]() and
and ![]() . What is the area of the inner square
. What is the area of the inner square ![]() ?
?
![]()
Solution
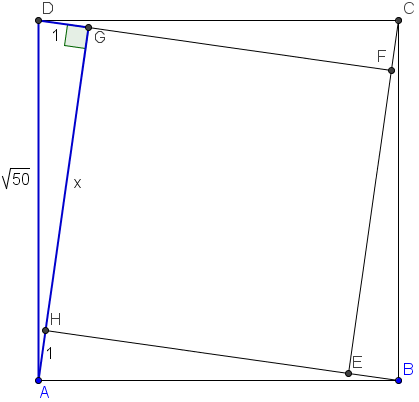
Arguable the hardest part of this question is to visualize the diagram. Since each side of ![]() can be extended to pass through a vertex of
can be extended to pass through a vertex of ![]() , we realize that
, we realize that ![]() must be tilted in such a fashion. Let a side of
must be tilted in such a fashion. Let a side of ![]() be
be ![]() .
.
Notice the right triangle (in blue) with legs ![]() and hypotenuse
and hypotenuse ![]() . By the Pythagorean Theorem, we have
. By the Pythagorean Theorem, we have ![]() . Thus,
. Thus, ![]()
Solution
You can also notice that the four triangles ![]() are congruent because the right angles of square
are congruent because the right angles of square ![]() cause them to be similar, and the hypotenuse of the triangles are the same because they are the sides of the square. Then you have
cause them to be similar, and the hypotenuse of the triangles are the same because they are the sides of the square. Then you have ![]() Solution by wxl18
Solution by wxl18
See also
| 2005 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 6 |
Followed by Problem 8 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()