1997 PMWC Problems/Problem I15
Problem
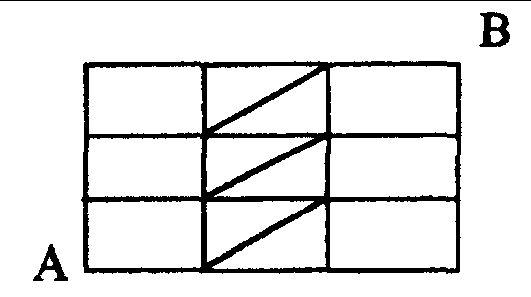
How many paths from A to B consist of exactly six line segments (vertical, horizontal or inclined)?
Solution
- Ignoring the diagonal segments, there are
paths. - Traversing the diagonals, we quickly find that the path must run through exactly 2 diagonals. There are
pairs of diagonals through which this is possible; quick counting shows us that each pair of diagonals yields 2 paths. So there are 6 more cases here.
paths.
pairs of diagonals through which this is possible; quick counting shows us that each pair of diagonals yields 2 paths. So there are 6 more cases here.In total, we get 
paths.
See also
| 1997 PMWC (Problems) | ||
| Preceded by Problem I14 |
Followed by Problem T1 | |
| I: 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 T: 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 | ||
