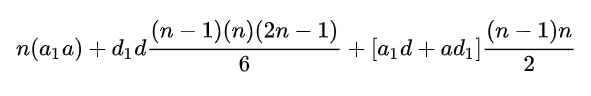Jadhav Arithmetic Merging Equation
Jadhav Arithmetic Merging Equation or Jadhav's Summation is a Mathematical Formula which can do summation of a finite arithmetic series whose terms are the result of product of respective terms of two arithmetic series with constant common difference (arithmetic progression). Derived by Indian Mathematician Jyotiraditya Abhay Jadhav.
Formula
Let us consider two different arithmetic progression series.
![]()
![]()
Now the series formed by product of their respective terms will be
![]()
So the summation of all the terms will be
![]()
Giving the Jadhav Arithmetic Merging Equation
![]()
Nomenclature
- n : Total number of terms in the corresponding series
- a : First term of first series
 : First term of second series
: First term of second series- d : Common difference of first series
 : Common difference of second series
: Common difference of second series
History
Been known Jyotiraditya Jadhav was trying to find a Generalized formula to easily apply factorial function to any number which was as superior as Isaac Newton's Binomial Theorem and came across a situation of multivariate binomials and was necessary to find their product to complete Factorial Equation and so started finding direct numerical patterns to complete it but was pretty unsuccessful in it and hence started with algebraic patterns and made Jadhav Arithmetic Merging Equation over-night.
Read More about Jyotiraditya Jadhav here
Practical Observation
Let us take series of 1,2,3.....10
And the second series of 1,3,5.....19
Now sum of product of respective terms will be using Jadhav Arithmetic Merging Equation gives :
![]()
and this works for any arithmetic series in real numbers.
Derivation
Let the two arithmetic series be
![]()
![]()
![]()
and sum of all the terms of this third series will be
![]()
Now we can use foil method to open-up brackets and get each term.
![]()
Now using laws of algebra and formula of sum of squares of Arithmetic Series we get,
![]()
Hence Deriving and Proving Jadhav Arithmetic Merging Equation.