Trigonometry
In geometry, Trigonometry is the study of the trigonometric functions, functions that seek to relate the lengths and angles of triangles. Trigonometry is integral to geometry, as many famous results were proven using trigonometry.
In contest math, trigonometry's use is not just limited to geometry; problems involving equations with trigonometric functions are very common. These are often solved via clever usage of the trigonometric functions' many identities, which drastically simplify expressions.
Outside of competition math, trigonometry is the backbone of much of analysis, especially Fourier analysis.
Right triangle definition
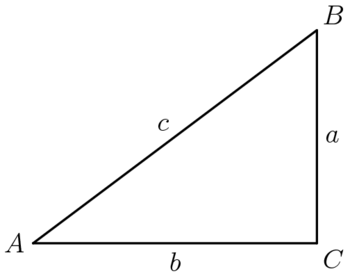
The right triangle definition of trigonometry involves the ratios between edges of a right triangle, with respect to a given angle. The definitions below will be referring to angle ![]() , with side lengths specified in the diagram.
, with side lengths specified in the diagram.
- Sine: The sine of angle
 , denoted
, denoted  , is defined as the ratio of the side opposite
, is defined as the ratio of the side opposite  to the hypotenuse;
to the hypotenuse; ![\[\sin (A) = \frac{\textrm{opposite}}{\textrm{hypotenuse}} = \frac{a}{c}.\]](//latex.artofproblemsolving.com/d/5/1/d51e2595afd41ed1215c94b583995eb3a8a64ce9.png)
- Cosine: The sine of angle
 , denoted
, denoted  , is defined as the ratio of the side adjacent
, is defined as the ratio of the side adjacent  to the hypotenuse;
to the hypotenuse; ![\[\cos (A) = \frac{\textrm{adjacent}}{\textrm{hypotenuse}} = \frac{b}{c}.\]](//latex.artofproblemsolving.com/0/2/f/02f541010fd15cff8b523abb6d34671297b1a84e.png)
- Tangent: The tangent of angle
 , denoted
, denoted  , is defined as the ratio of the side opposite
, is defined as the ratio of the side opposite  to the side adjacent to
to the side adjacent to  ;
; ![\[\tan (A) = \frac{\textrm{opposite}}{\textrm{adjacent}} = \frac{a}{b}.\]](//latex.artofproblemsolving.com/0/8/8/0888d2ff5bf0883f98414b16fc23db4cc9d4afd3.png)
A common mneumonic to remember this is SOH-CAH-TOA, where Sine = Opposite / Hypotenuse, Cosine = Adjacent / Hypotenuse Tangent = Opposite / Adjacent
More uncommon are the reciprocals of the trigonometric functions, listed below.
- Cosecant: The cosecant of angle
 , denoted
, denoted  , is defined as the reciprocal of the sine of
, is defined as the reciprocal of the sine of  ;
; ![\[\csc (A) = \frac{1}{\sin (x)} = \frac{\textrm{hypotenuse}}{\textrm{opposite}} = \frac{c}{a}.\]](//latex.artofproblemsolving.com/6/e/8/6e85922c401a089d47d99982a02ad3043b772d45.png)
- Secant: The secant of angle
 , denoted
, denoted  , is defined as the reciprocal of the cosine of
, is defined as the reciprocal of the cosine of  ;
; ![\[\sec (A) = \frac{1}{\cos (x)} = \frac{\textrm{hypotenuse}}{\textrm{adjacent}} = \frac{c}{b}.\]](//latex.artofproblemsolving.com/1/f/1/1f1760b80f18ba4905e623ad69a3126618a8f7e3.png)
- Cotangent: The cotangent of angle
 , denoted
, denoted  , is defined as the reciprocal of the tangent of
, is defined as the reciprocal of the tangent of  ;
; ![\[\cot (A) = \frac{1}{\tan (x)} = \frac{\textrm{adjacent}}{\textrm{opposite}} = \frac{b}{a}.\]](//latex.artofproblemsolving.com/9/5/e/95e4a8e2ca2ac416da133b5ffe8a5be32117dd28.png)
Unit Circle Definition
Consider the unit circle, the circle with radius one centered at the origin. By picking a point on the circle, and dropping a perpendicular line to the x-axis, a right triangle is formed with a hypotenuse 1 unit long. Letting the angle at the origin be ![]() and the coordinates of the point we picked to be
and the coordinates of the point we picked to be ![]() , we have:
, we have:

Note that ![]() is the rectangular coordinates for the point
is the rectangular coordinates for the point ![]() .
.
This is true for all angles, even negative angles and angles greater than 360 degrees. Due to the way trig ratios are defined for non-acute angles, the value of a trig ratio could be positive or negative, or even 0.