2005 IMO Shortlist Problems/G3
Problem
(Ukraine)
Let ![]() be a parallelogram. A variable line
be a parallelogram. A variable line ![]() passing through the point
passing through the point ![]() intersects the rays
intersects the rays ![]() and
and ![]() at points
at points ![]() and
and ![]() , respectively. Let
, respectively. Let ![]() and
and ![]() be the centres of the excircles of triangles
be the centres of the excircles of triangles ![]() and
and ![]() , touching the sides
, touching the sides ![]() and
and ![]() , respectively. Prove that the size of angle
, respectively. Prove that the size of angle ![]() does not depend on the choice of
does not depend on the choice of ![]() .
.
This was also Problem 3 of the 2006 3rd German TST, and a problem at the 2006 India IMO Training Camp. It also appeared in modified form as Problem 3, Day 3 of the 2006 Iran TST.
Solution
Let ![]() be the interior angle bisectors of
be the interior angle bisectors of ![]() . Let
. Let ![]() be the exterior angle bisectors of
be the exterior angle bisectors of ![]() . Then
. Then ![]() is the intersection of
is the intersection of ![]() and
and ![]() is the intersection of
is the intersection of ![]() .
.
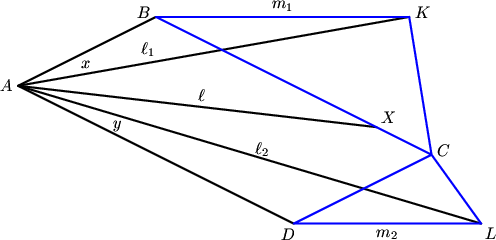
Let us denote ![]() as the measures of
as the measures of ![]() , and denote
, and denote ![]() . Then
. Then ![]() . Furthermore, since
. Furthermore, since ![]() is the exterior angle bisector of
is the exterior angle bisector of ![]() , we know that the exterior angle at
, we know that the exterior angle at ![]() is
is ![]() , so
, so ![]() . Similarly,
. Similarly, ![]() . It follows that triangles
. It follows that triangles ![]() are similar. Then since
are similar. Then since ![]() is a parallelogram,
is a parallelogram,
![]() .
.
Since we know ![]() , this implies that triangles
, this implies that triangles ![]() are similar. This means that
are similar. This means that
![]()
![]() ,
,
which is independent of ![]() , since
, since ![]() is always half the measure of
is always half the measure of ![]() . ∎
. ∎
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.









