2007 Cyprus MO/Lyceum/Problem 25

Problem

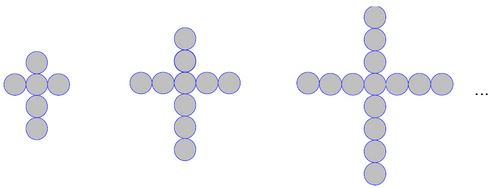
A jeweller makes crosses, according to the pattern shown above. The crosses are made from golden cyclical discs, with diameter of 1cm each. The height of a cross, which is made from 402 such discs is

$\mathrm{(A) \ } 198cm\qquad \mathrm{(B) \ } 2m\qquad \mathrm{(C) \ } 201cm\qquad \mathrm{(D) \ } 202cm\qquad \mathrm{(E) \ } 204cm$

Solution

If $n$ represents the number of the cross, then there are $4n + 2$ disks in the cross ( $4n$ to count for the 4 legs of the cross, plus one for the center and one for the bottom leg). So $\displaystyle 4n+2=402 \Rightarrow n = 100$ . The number of discs from top to bottom is $2n + 2 = 202 \Longrightarrow \mathrm{D}$ .

2007 Cyprus MO, Lyceum (Problems)
Preceded by Problem 24	Followed by Problem 26
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30

Page

Toolbox

Search

2007 Cyprus MO/Lyceum/Problem 25

Problem

Solution

See also