2003 AMC 10A Problems/Problem 19

Problem

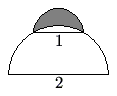
A semicircle of diameter $1$ sits at the top of a semicircle of diameter $2$ , as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.

$\mathrm{(A) \ } \frac{1}{6}\pi-\frac{\sqrt{3}}{4}\qquad \mathrm{(B) \ } \frac{\sqrt{3}}{4}-\frac{1}{12}\pi\qquad \mathrm{(C) \ } \frac{\sqrt{3}}{4}-\frac{1}{24}\pi\qquad \mathrm{(D) \ } \frac{\sqrt{3}}{4}+\frac{1}{24}\pi\qquad \mathrm{(E) \ } \frac{\sqrt{3}}{4}+\frac{1}{12}\pi$

Solution

The shaded area is equal to the area of the smaller semicircle minus the area of a sector of the larger circle plus the area of a triangle formed by two radii of the larger semicircle and the diameter of the smaller semicircle.

The area of the smaller semicircle is $\frac{1}{2}\pi\cdot(\frac{1}{2})^{2}=\frac{1}{8}\pi$ .

Since the radius of the larger semicircle is equal to the diameter of the smaller semicircle, the triangle is an equilateral triangle and the sector measures $60^\circ$ .

The area of the $60^\circ$ sector of the larger semicircle is $\frac{60}{360}\pi\cdot(\frac{2}{2})^{2}=\frac{1}{6}\pi$ .

The area of the triangle is $\frac{1^{2}\sqrt{3}}{4}=\frac{\sqrt{3}}{4}$

So the shaded area is $\frac{1}{8}\pi-\frac{1}{6}\pi+\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}-\frac{1}{24}\pi \Rightarrow C$

Page

Toolbox

Search

2003 AMC 10A Problems/Problem 19

Problem

Solution

See Also