1987 AIME Problems/Problem 15

Problem

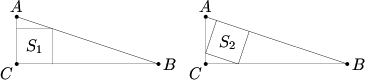
Squares $S_1$ and $S_2$ are inscribed in right triangle $ABC$ , as shown in the figures below. Find $AC + CB$ if area $(S_1) = 441$ and area $(S_2) = 440$ .

Solution

Because all the triangles in the figure are similar to triangle $ABC$ , it's a good idea to use area ratios. In the diagram above, $\frac {T_1}{T_3} = \frac {T_2}{T_4} = \frac {441}{440}.$ Hence, $T_3 = \frac {440}{441}T_1$ and $T_4 = \frac {440}{441}T_2$ . Additionally, the area of triangle $ABC$ is equal to both $T_1 + T_2 + 441$ and $T_3 + T_4 + T_5 + 440.$

Setting the equations equal and solving for $T_5$ , $T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}$ . Therefore, $441T_5 = 441 + T_1 + T_2$ . However, $441 + T_1 + T_2$ is equal to the area of triangle $ABC$ ! This means that the ratio between the areas $T_5$ and $ABC$ is $441$ , and the ratio between the sides is $\sqrt {441} = 21$ . As a result, $AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}$ . We now need $(AC)(BC)$ to find the value of $AC + BC$ , because $AB^2 + 2(AC)(BC) = (AC + BC)^2$ .

Let $h$ denote the height to the hypotenuse of triangle $ABC$ . Notice that $h - \frac {1}{21}h = \sqrt {440}$ . (The height of $ABC$ decreased by the corresponding height of $T_5$ ) Thus, $(AB)(h) = (AC)(BC) = 22\cdot 21^2$ . Because $AB^2 + 2(AC)(BC) = (AC + BC)^2 = 21^2\cdot22^2$ , $AC + BC = (21)(22) = \boxed{462}$ .

1987 AIME (Problems • Answer Key • Resources)
Preceded by Problem 14	Followed by Last Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

1987 AIME Problems/Problem 15

Problem

Solution

See also