1971 Canadian MO Problems
This is an empty template page which needs to be filled. You can help us out by finding the needed content and editing it in. Thanks.
Contents
Problem 1
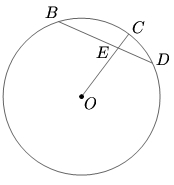
![]() is a chord of a circle such that
is a chord of a circle such that ![]() and
and ![]() Let
Let ![]() be the center of the circle. Join
be the center of the circle. Join ![]() and extend
and extend ![]() to cut the circle at
to cut the circle at ![]() Given
Given ![]() find the radius of the circle
find the radius of the circle
Problem 2
Let ![]() and
and ![]() be positive real numbers such that
be positive real numbers such that ![]() . Show that
. Show that ![]() .
.
Problem 3
![]() is a quadrilateral with
is a quadrilateral with ![]() . If
. If ![]() is greater than
is greater than ![]() , prove that
, prove that ![]() .
.
Problem 4
Determine all real numbers ![]() such that the two polynomials
such that the two polynomials ![]() and
and ![]() have at least one root in common.
have at least one root in common.
Problem 5
Let ![]() , where the coefficients
, where the coefficients ![]() are integers. If
are integers. If ![]() and
and ![]() are both odd, show that
are both odd, show that ![]() has no integral roots.
has no integral roots.
Problem 6
Show that, for all integers ![]() ,
, ![]() is not a multiple of 121.
Solution
is not a multiple of 121.
Solution