2003 AMC 12A Problems/Problem 13

Problem

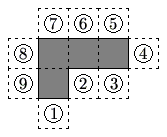
The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attatched to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?

$\mathrm{(A) \ } 2\qquad \mathrm{(B) \ } 3\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } 5\qquad \mathrm{(E) \ } 6$

Solution

Let the squares be labeled $A$ , $B$ , $C$ , and $D$ .

When the polygon is folded, the "right" edge of square $A$ becomes adjacent to the "bottom edge" of square $C$ , and the "bottom" edge of square $A$ becomes adjacent to the "bottom" edge of square $D$ .

So, any "new" square that is attatched to those edges will prevent the polygon from becoming a cube with one face missing.

Therefore, squares $1$ , $2$ , and $3$ will prevent the polygon from becoming a cube with one face missing.