2002 AMC 12B Problems/Problem 20
Problem
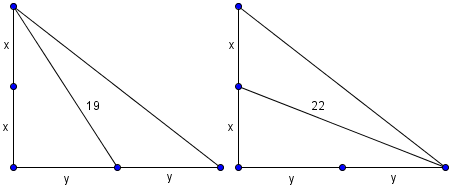
Let ![]() be a right-angled triangle with
be a right-angled triangle with ![]() . Let
. Let ![]() and
and ![]() be the midpoints of legs
be the midpoints of legs ![]() and
and ![]() , respectively. Given that
, respectively. Given that ![]() and
and ![]() , find
, find ![]() .
.
![]()
Solution
Let ![]() ,
, ![]() . By the Pythagorean Theorem on
. By the Pythagorean Theorem on ![]() respectively,
respectively,
![]()
Summing these gives ![]() .
.
By the Pythagorean Theorem again, we have
![]()
See also
| 2002 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 19 |
Followed by Problem 21 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |