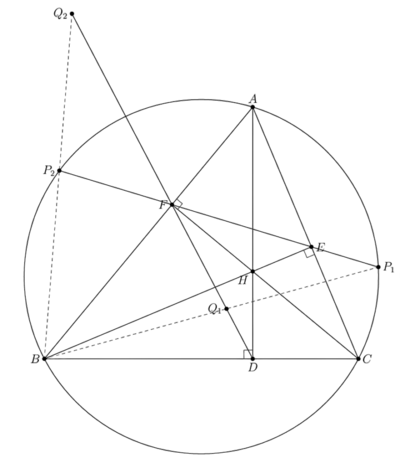
2010 IMO Shortlist Problems/G1

Problem

(United Kingdom) Let $ABC$ be an acute triangle with $D$ , $E$ , $F$ the feet of the altitudes lying on $BC$ , $CA$ , $AB$ respectively. One of the intersection points of the line $EF$ and the circumcircle is $P$ . The lines $BP$ and $DF$ meet at point $Q$ . Prove that $AP = AQ$ .

Solution

Let $\measuredangle$ denote directed angles modulo $180^{\circ}$ . As $\measuredangle AFC = \measuredangle ADC = 90^{\circ}$ , $AFDC$ is cyclic.

As $APBC$ and $AFDC$ are both cyclic,

$\measuredangle QPA = \measuredangle BPA = \measuredangle BCA = \measuredangle DCA = \measuredangle DFA = \measuredangle QFA$ .

Therefore, we see $AFPQ$ is cyclic. Then

$\measuredangle AQP = \measuredangle AFP = \measuredangle AFE = \measuredangle AHE = \measuredangle DHE = \measuredangle DCE = \measuredangle BCA$ .

We deduce that $\measuredangle AQP = \measuredangle BCA = \measuredangle QPA$ , which is enough to apply that $\bigtriangleup APQ$ is isosceles with $AP = AQ$ .

(Note that with directed angles in place, both the two possible configurations (shown in graph) are solved.)

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

Resources

Page

Toolbox

Search

2010 IMO Shortlist Problems/G1

Problem

Solution

Resources