2014 AMC 10A Problems/Problem 22

1 Problem
2 Solution 1 (Trigonometry)
3 Solution 2 (No Trigonometry)
4 Solution 3 Quick Construction (No Trigonometry)
5 Solution 4 (No Trigonometry)
6 Solution 5
7 Solution 6 (Pure Euclidian Geometry)
8 Solution 7 (Pure Euclidian Geometry)
9 Solution 8 (Trigonometry)
10 Solution 9
11 Solution 10 Law of Cosines
12 Video Solution by Richard Rusczyk
13 See Also

Problem

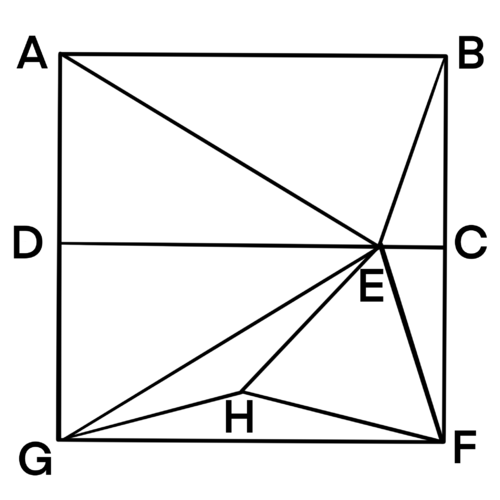
In rectangle $ABCD$ , $\overline{AB}=20$ and $\overline{BC}=10$ . Let $E$ be a point on $\overline{CD}$ such that $\angle CBE=15^\circ$ . What is $\overline{AE}$ ?

$\textbf{(A)}\ \dfrac{20\sqrt3}3\qquad\textbf{(B)}\ 10\sqrt3\qquad\textbf{(C)}\ 18\qquad\textbf{(D)}\ 11\sqrt3\qquad\textbf{(E)}\ 20$

Solution 1 (Trigonometry)

Note that $\tan 15^\circ=2-\sqrt{3}=\frac{EC}{10} \Rightarrow EC=20-10 \sqrt 3$ . (It is important to memorize the sin, cos, and tan values of $15^\circ$ and $75^\circ$ .) Therefore, we have $DE=10\sqrt 3$ . Since $ADE$ is a $30-60-90$ triangle, $AE=2 \cdot AD=2 \cdot 10=\boxed{\textbf{(E)} \: 20}$

Solution 2 (No Trigonometry)

Let $F$ be a point on line $\overline{CD}$ such that points $C$ and $F$ are distinct and that $\angle EBF = 15^\circ$ . By the angle bisector theorem, $\frac{BC}{BF} = \frac{CE}{EF}$ . Since $\triangle BFC$ is a $30-60-90$ right triangle, $CF = \frac{10\sqrt{3}}{3}$ and $BF = \frac{20\sqrt{3}}{3}$ . Additionally, $CE + EF = CF = \frac{10\sqrt{3}}{3}$ Now, substituting in the obtained values, we get $\frac{10}{\frac{20\sqrt{3}}{3}} = \frac{CE}{EF} \Rightarrow \frac{2\sqrt{3}}{3}CE = EF$ and $CE + EF = \frac{10\sqrt{3}}{3}$ . Substituting the first equation into the second yields $\frac{2\sqrt{3}}{3}CE + CE = \frac{10\sqrt{3}}{3} \Rightarrow CE = 20 - 10\sqrt{3}$ , so $DE = 10\sqrt{3}$ . Because $\triangle ADE$ is a $30-60-90$ triangle, $AE = \boxed{\textbf{(E)}~20}$ .

~edited by ripkobe_745

Solution 3 Quick Construction (No Trigonometry)

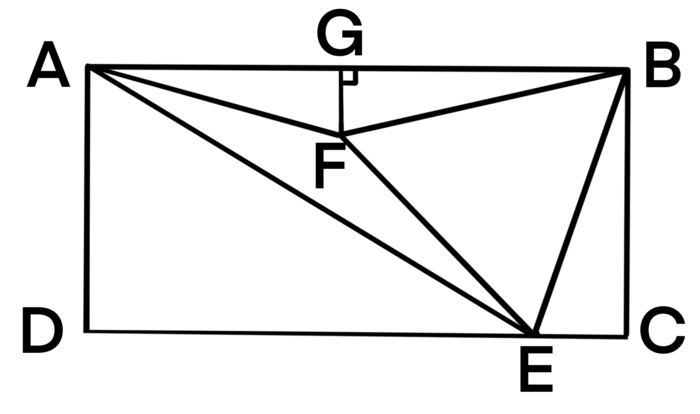
Reflect $\triangle{ECB}$ over line segment $\overline{CD}$ . Let the point $F$ be the point where the right angle is of our newly reflected triangle. By subtracting $90 - (15+15) = 60$ to find $\angle ABF$ , we see that $\triangle{ABC}$ is a $30-60-90$ right triangle. By using complementary angles once more, we can see that $\angle{EAD}$ is a $60^\circ$ angle, and we've found that $\triangle{EAD}$ is a $30-60-90$ right triangle. From here, we can use the $1-2-\sqrt{3}$ properties of a $30-60-90$ right triangle to see that $\overline{AE}=\boxed{\textbf{(E)}~20}.$

Solution 4 (No Trigonometry)

Let $F$ be a point on $BC$ such that $\angle{FEC}=60^{\circ}$ . Then $\angle{BEF}=\angle{BEC}-\angle{FEC}=15^{\circ}$ Since $\angle{BEF}=\angle{EBF}$ , $\bigtriangleup{BFE}$ is isosceles.

Let $CF=x$ . Since $\bigtriangleup{FEC}$ is $60^{\circ}-90^{\circ}-30^{\circ}$ , we have $EF=\frac{2}{\sqrt{3}}x$

Since $\bigtriangleup{BFE}$ is isosceles, we have $BF=EF=\frac{2}{\sqrt{3}}x$ . Since $BF+FC=BF$ , we have $\frac{2}{\sqrt{3}}x+x=10 \Longrightarrow x=20\sqrt{3}-30$ Thus $EC=\frac{1}{\sqrt{3}}BC=20-10\sqrt{3}$ and $DE=DC-EC=20-EC=10\sqrt{3}$ .

Finally, by the Pythagorean Theorem, we have $AE=\sqrt{AD^2+DE^2}=\sqrt{10^2+(10\sqrt{3})^2}=20 \boxed{\mathrm{(E)}}$

~ Solution by Nafer

~ Edited by TheBeast5520

Note from williamgolly: When you find DE, note how ADE is congruent to a 30-60-90 triangle and you can easily find AE from there

Solution 5

First, divide all side lengths by $10$ to make things easier. We’ll multiply our answer by $10$ at the end. Call side length $BE$ $x$ . Using the Pythagorean Theorem, we can get side $EC$ is $\sqrt{x^2-1}$ .

The double angle identity for sine states that: $\sin{2a} = 2 \sin{a}\cdot \cos{a}$ So, $\sin 30 = 2\sin 15\cdot \cos 15$ We know $\sin 30 = \frac{1}{2}$ . In triangle $BEC$ , $\sin 15 = \frac{\sqrt{x^2-1}}{x}$ and $\cos 15 = \frac{1}{x}$ . Substituting these in, we get our equation: $\frac{1}{2} = 2 \cdot \frac{\sqrt{x^2-1}}{x} \cdot \frac{1}{x}$ which simplifies to $x^4-16x^2+16 = 0$

Now, using the quadratic formula to solve for $x^2$ . $x^2 = 16 \pm \frac{\sqrt{16^2-4\cdot16}}{2} = 8 \pm 4\sqrt3$ Because the length $BE$ must be close to one, the value of $x^2$ will be $8-4\sqrt3$ . We can now find $EC$ = $\sqrt{x^2-1} = \sqrt{7-4\sqrt3} = 2-\sqrt3$ and use it to find $DE$ . $DE = 2-EC = \sqrt3$ . To find $AE$ , we can use the Pythagorean Theorem with sides $AD$ and $DE$ , OR we can notice that, based on the two side lengths we know, $ADE$ is a $30-60-90$ triangle. So $AE = 2\cdot AD = 2$ .

Finally, we must multiply our answer by $10$ , $2\cdot 10 = 20$ . $\boxed{\textbf{(E)}}$ .

~AWCHEN01

Solution 6 (Pure Euclidian Geometry)

We are going to use pure Euclidian geometry to prove $AE=AB$ .

Reflect rectangle $ABCD$ along line $CD$ . Let the square be $ABFG$ as shown. Construct equilateral triangle $\triangle EFH$ .

Because $HF=EF$ , $GF=BF=20$ , and $\angle GFH=\angle BFE=15^{\circ}$ , $\triangle GFH\cong \triangle BFE$ by $SAS$ .

So, $GH=BE$ , $GH=HE=HF$ .

Because $GH=HE=HF$ , $\angle GHF= \angle BEF=75^{\circ} + 75^{\circ} = 150^{\circ}$ , $\angle GHE=360^{\circ}-150^{\circ}-60^{\circ}=150^{\circ}$ , $\angle GHE=\angle GHF$ .

$\triangle GHE \cong \triangle GHF$ by $SAS$ .

So, $GF=GE$ . By the reflection, $AE=GE=GF=AB$ . $AE=AB=\boxed{\textbf{(E)}~20}$

This solution is inspired by AoPS "Introduction to Geometry" page 226 problem 8.22, and page 433 problem 16.42.

~isabelchen

Solution 7 (Pure Euclidian Geometry)

We are going to use pure Euclidian geometry to prove $AE=AB$ .

Construct equilateral triangle $\triangle BEF$ , and let $GF$ be the height of $\triangle ABF$ .

$\angle GBF=90^{\circ}-15^{\circ}-60^{\circ}=15^{\circ}$ , $\angle GBF=\angle CBE$ , $\angle BGF=\angle BCE=90^{\circ}$ , $BF=BE$ .

$\triangle BGF \cong \triangle BCE$ by $AAS$ .

$BG=BC=10, AG=20-10=10$ , $AG=BG$ , $GF=GF$ , by $HL$ $\triangle AGF \cong \triangle BGF$ .

So, $AF=BF=EF$ .

$\angle AFB=75^{\circ}+75^{\circ}=150^{\circ}$ , $\angle AFE=360^{\circ}-150^{\circ}-60^{\circ}=150^{\circ}$ , $\angle AFB=\angle AFE$ , $AF=AF$ , $BF=EF$ .

$\triangle AFB \cong \triangle AFE$ by $SAS$ .

So, $AE=AB=\boxed{\textbf{(E)}~20}$

Note: Similar to previous Solution

~isabelchen

Solution 8 (Trigonometry)

All trigonometric functions in this solution are in degrees. We know $\sin\left(a+b\right)=\sin\left(a\right)\cos\left(b\right)+\sin\left(b\right)\cos\left(a\right)$ so $\sin\left(15\right)=\sin\left(45-30\right)=\sin\left(45\right)\cos\left(-30\right)+\sin\left(-30\right)\cos\left(45\right)$ $=\frac{\sqrt{2}}{2}\cdot\left(-\frac{\sqrt{3}}{2}\right)+\frac{1}{2}\cdot\frac{\sqrt{2}}{2}=\frac{-\sqrt{6}}{4}+\frac{\sqrt{2}}{4}=\frac{\sqrt{2}-\sqrt{6}}{4}$ $=\frac{\sqrt{2}-\sqrt{6}}{4}$ Let $EC=x$ , then $BE=\sqrt{x^{2}+100}$ . By the definition of sine, $\frac{x}{\sqrt{x^{2}+100}}=\frac{\sqrt{2}-\sqrt{6}}{4}$ Squaring both sides, $\frac{x^{2}}{x^{2}+100}=\frac{\left(\sqrt{2}-\sqrt{6}\right)^{2}}{16}=\frac{2-2\sqrt{12}+6}{16}=\frac{8-4\sqrt{3}}{16}=\frac{2-\sqrt{3}}{4}$ Cross-multiplying, $4x^{2}=\left(2-\sqrt{3}\right)\left(x^{2}+100\right)=2x^{2}+200-\sqrt{3}x^{2}-100\sqrt{3}$ Simplifying, $\left(2+\sqrt{3}\right)x^{2}=200-100\sqrt{3}$ $x^{2}=\frac{200-100\sqrt{3}}{2+\sqrt{3}}=\frac{100\left(2-\sqrt{3}\right)}{2+\sqrt{3}}=100\cdot\frac{2-\sqrt{3}}{2+\sqrt{3}}$ Let $\frac{2-\sqrt{3}}{2+\sqrt{3}}=p$ . Notice that $\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=2^{2}-\sqrt{3}^{2}=1$ so $2-\sqrt{3}=\frac{1}{2+\sqrt{3}}$ . $p$ is then $\frac{2-\sqrt{3}}{2+\sqrt{3}}=\frac{\frac{1}{2+\sqrt{3}}}{2+\sqrt{3}}=\frac{1}{\left(2+\sqrt{3}\right)^{2}}$ Recall that $x^{2}=100\cdot\frac{2-\sqrt{3}}{2+\sqrt{3}}$ which we now know is $100\cdot\frac{1}{\left(2+\sqrt{3}\right)^{2}}=\frac{100}{\left(2+\sqrt{3}\right)^{2}}=\left(\frac{10}{2+\sqrt{3}}\right)^{2}$ Therefore $x=\frac{10}{2+\sqrt{3}}$ Rationalizing the denominator, $\frac{10}{2+\sqrt{3}}\cdot\frac{2-\sqrt{3}}{2-\sqrt{3}}=\frac{20-10\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}$ Which by difference of squares reduces to $20-10\sqrt{3}$ so $EC=20-10\sqrt{3}$ . $ED$ is then $20-\left(20-10\sqrt{3}\right)=10\sqrt{3}$ and since we know $AD=10$ , by the Pythagorean theorem, $AE = 20$ . The answer is $\boxed{\textbf{(E)}~20}$

An alternate way to finish: since we know the lengths of $AD$ and $DE$ , we can figure out that $m\angle AED=30^{\circ}$ and therefore $m\angle BEA=75^{\circ}$ . Hence $\triangle ABE$ is isosceles and $AE=AB=\boxed{\textbf{(E)}~20}$ .

~JH. L

Solution 9

Similar to the others except that you find the base of the 15-75-90 triangle knowing that the side opposite side to 75 is 10, finding that you can subtract to find the base of the rectangle of the diagonal we are trying to find.

~YBSuburbanTea

Solution 10 Law of Cosines

The ratio between the side lengths of a 15, 75, 90 triangle are \sqrt{3}-1, \sqrt(3)+1, 2\sqrt(2).

we have $DE=10\sqrt 3$

Video Solution by Richard Rusczyk

https://www.youtube.com/watch?v=-GBvCLSfTuo

2014 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 21	Followed by Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search