1988 AIME Problems/Problem 12
Problem
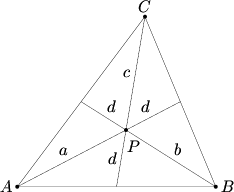
Let ![]() be an interior point of triangle
be an interior point of triangle ![]() and extend lines from the vertices through
and extend lines from the vertices through ![]() to the opposite sides. Let
to the opposite sides. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() denote the lengths of the segments indicated in the figure. Find the product
denote the lengths of the segments indicated in the figure. Find the product ![]() if
if ![]() and
and ![]() .
.
Solution 1
Call the cevians AD, BE, and CF. Using area ratios (![]() and
and ![]() have the same base), we have:
have the same base), we have:
![]()
Similarily, ![]() and
and ![]() .
.
Then,
![]()
The identity ![]() is a form of Ceva's Theorem.
is a form of Ceva's Theorem.
Plugging in ![]() , we get
, we get
![]()
![]()
![]()
![]()
Solution 2
Let ![]() be the weights of the respective vertices. We see that the weights of the feet of the cevians are
be the weights of the respective vertices. We see that the weights of the feet of the cevians are ![]() . By mass points, we have that:
. By mass points, we have that: ![]()
![]()
![]()
If we add the equations together, we get ![]()
If we multiply them together, we get ![]()
Solution 3
You can use mass points to derive ![]() Plugging it in yields
Plugging it in yields ![]() We proceed as we did in Solution 1 - however, to make the equation look less messy, we do the substitution
We proceed as we did in Solution 1 - however, to make the equation look less messy, we do the substitution ![]()
Then we have ![]() Clearing fractions gives us
Clearing fractions gives us ![]() Factoring yields
Factoring yields ![]() and the left hand side looks suspiciously like what we want to find. (It is.)
and the left hand side looks suspiciously like what we want to find. (It is.)
Substituting yields our answer as ![]()
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.