Gossard perspector

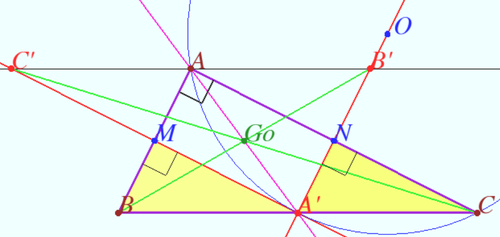
Gossard perspector X(402) and Gossard triangle

In $1765$ Leonhard Euler proved that in any triangle, the orthocenter, circumcenter and centroid are collinear. We name this line the Euler line. Soon he proved that the Euler line of a given triangle together with two of its sides forms a triangle whose Euler line is in parallel with the third side of the given triangle.

Professor Harry Clinton Gossard in $1916$ proved that three Euler lines of the triangles formed by the Euler line and the sides, taken by two, of a given triangle, form a triangle which is perspective with the given triangle and has the same Euler line. The center of the perspective now is known as the Gossard perspector or the Kimberling point $X(402).$

Let triangle $\triangle ABC$ be given. The Euler line crosses lines $AB, BC,$ and $AC$ at points $D, E,$ and $F.$

On $13/01/2023$ it was found that the Gossard perspector is the centroid of the points $A, B, C, D, E, F.$

vladimir.shelomovskii@gmail.com, vvsss

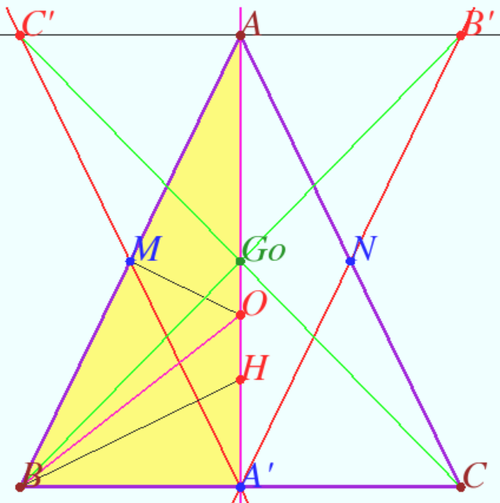
Gossard perspector of right triangle

It is clear that the Euler line of right triangle $ABC (\angle A = 90 ^\circ)$ meet the sidelines $BC, CA$ and $AB$ of $\triangle ABC$ at $A'$ and $A,$ where $A'$ is the midpoint of $BC.$

Let $\triangle A'B'C'$ be the triangle formed by the Euler lines of the $\triangle AA'B, \triangle AA'C,$ and the line $l$ contains $A$ and parallel to $BC,$ the vertex $B'$ being the intersection of the Euler line of the $\triangle AA'C$ and $l,$ the vertex $C'$ being the intersection of the Euler line of the $\triangle AA'B$ and $l.$

We call the triangle $\triangle A'B'C'$ as the Gossard triangle of $\triangle ABC.$

Let $\triangle ABC$ be any right triangle and let $\triangle A'B'C'$ be its Gossard triangle. Then the lines $AA', BB',$ and $CC'$ are concurrent. We call the point of concurrence $Go$ as the Gossard perspector of $\triangle ABC.$

$Go$ is the midpoint of $AA'.$ $A$ is orthocenter of $\triangle ABC, A'$ is circumcenter of $\triangle ABC,$ so $Go$ is midpoint of $OH.$

$M = A'C' \cap AB$ is the midpoint $AB, N = A'B' \cap AC$ is the midpoint $AC, \triangle A'BM = \triangle CNA' \sim \triangle CBA$ with coefficient $k = \frac {1}{2}.$

Any right triangle and its Gossard triangle are congruent.

Any right triangle and its Gossard triangle have the same Euler line.

The Gossard triangle of the right $\triangle ABC$ is the reflection of $\triangle ABC$ in the Gossard perspector.

vladimir.shelomovskii@gmail.com, vvsss

Gossard perspector and Gossard triangle for isosceles triangle

It is clear that the Euler line of isosceles $\triangle ABC (AB = AC)$ meet the sidelines $BC, CA$ and $AB$ of $\triangle ABC$ at $A'$ and $A,$ where $A'$ is the midpoint of $BC.$

Let $\triangle A'B'C'$ be the triangle formed by the Euler lines of the $\triangle AA'B, \triangle AA'C,$ and the line $l$ contains $A$ and parallel to $BC,$ the vertex $B'$ being the intersection of the Euler line of the $\triangle AA'C$ and $l,$ the vertex $C'$ being the intersection of the Euler line of the $\triangle AA'B$ and $l.$

We call the triangle $\triangle A'B'C'$ as the Gossard triangle of $\triangle ABC.$

Let $\triangle ABC$ be any isosceles triangle and let $\triangle A'B'C'$ be its Gossard triangle. Then the lines $AA', BB',$ and $CC'$ are concurrent. We call the point of concurrence $Go$ as the Gossard perspector of $\triangle ABC.$ Let $H$ be the orthocenter of $\triangle ABC, O$ be the circumcenter of $\triangle ABC.$

It is clear that $Go$ is the midpoint of $AA'.$ $M = A'C' \cap AB$ is the midpoint $AB, N = A'B' \cap AC$ is the midpoint $AC.$

$\triangle A'BM = \triangle CNA' \sim \triangle CBA$ with coefficient $k = \frac {1}{2}.$

Any isosceles triangle and its Gossard triangle are congruent.

Any isosceles triangle and its Gossard triangle have the same Euler line.

The Gossard triangle of the isosceles $\triangle ABC$ is the reflection of $\triangle ABC$ in the Gossard perspector. Denote $\angle BAC = \alpha, \angle ABC = \angle ACB = \beta, AO = BO = R \implies$ $\sin \beta = \cos \frac {\alpha}{2}, GoO = AO – AGo = R \cdot \frac{1 – \cos {\alpha}}{2},$ $OH = AH – AO = R(2 \cos \alpha – 1) \implies \vec {GoO} = \vec {OH} \cdot \frac {1 – \cos \alpha}{2(2 \cos \alpha – 1)}.$

vladimir.shelomovskii@gmail.com, vvsss

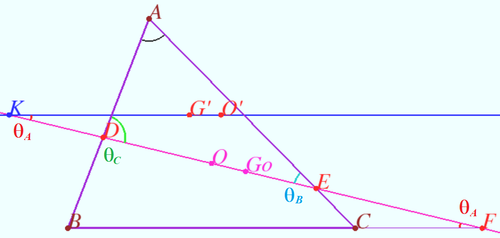
Euler line of the triangle formed by the Euler line and the sides of a given triangle

Let the Euler line of $\triangle ABC$ meet the sidelines $AB, AC,$ and $BC$ of $\triangle ABC$ at $D, E,$ and $F,$ respectively.

Euler line of the $\triangle ADE$ is parallel to $BC.$ Similarly, Euler line of the $\triangle BDF$ is parallel to $AC,$ Euler line of the $\triangle CEF$ is parallel to $AB.$

Proof

Denote $\angle A = \alpha, \angle B = \beta, \angle C = \gamma,$ smaller angles between the Euler line and lines $BC, AC,$ and $AB$ as $\theta_A, \theta_B,$ and $\theta_C,$ respectively. WLOG, $AC > BC > AB.$ It is known that $\tan \theta_A = \frac{3 – \tan \beta \cdot \tan \gamma}{\tan \beta – \tan \gamma}, \tan \theta_B = \frac{3 – \tan \alpha \cdot \tan \gamma}{\tan \alpha – \tan \gamma}, \tan \theta_C = \frac{3 – \tan \beta \cdot \tan \alpha}{\tan \beta – \tan \alpha}.$

Euler line

Let $O'$ be circumcenter of $\triangle ADE, KO'$ be Euler line of $\triangle ADE, K \in DE$ (line).

Similarly, $\tan \angle O'KF = \frac{3 – \tan \theta_B \cdot \tan \theta_C}{\tan \theta_C – \tan \theta_B}.$ $3(\tan\alpha – \tan \gamma) (\tan\alpha – \tan \beta) – (3 – \tan \alpha \cdot \tan \gamma) (3 – \tan \alpha \cdot \tan \beta) = (\tan^2 \alpha – 3) \cdot (3 –\tan \beta \cdot \tan \gamma),$ $(3 – \tan \alpha \cdot \tan \gamma) \cdot (\tan\alpha – \tan \beta) – (3 – \tan \alpha \cdot \tan \beta) \cdot (\tan\alpha – \tan \gamma) = (\tan^2 \alpha – 3) \cdot (\tan \beta – \tan \gamma).$ Suppose, $\tan^2 \alpha \ne 3$ which means $\alpha \ne 60^\circ$ and $\alpha \ne 120^\circ.$ In this case $\tan \angle O'KF = \frac{3 – \tan \beta \cdot \tan \gamma}{\tan \beta – \tan \gamma} = \tan \theta_A \implies \angle O'KF = \theta_A \implies O'K||BC.$