2022 AMC 12B Problems/Problem 25

Problem

Four regular hexagons surround a square with side length 1, each one sharing an edge with the square, as shown in the figure below. The area of the resulting 12-sided outer nonconvex polygon can be written as $m \sqrt{n} + p$ , where $m$ , $n$ , and $p$ are integers and $n$ is not divisible by the square of any prime. What is $m+n+p$ ? $[asy] import geometry; unitsize(3cm); draw((0,0) -- (1,0) -- (1,1) -- (0,1) -- cycle); draw(shift((1/2,1-sqrt(3)/2))*polygon(6)); draw(shift((1/2,sqrt(3)/2))*polygon(6)); draw(shift((sqrt(3)/2,1/2))*rotate(90)*polygon(6)); draw(shift((1-sqrt(3)/2,1/2))*rotate(90)*polygon(6)); draw((0,1-sqrt(3))--(1,1-sqrt(3))--(3-sqrt(3),sqrt(3)-2)--(sqrt(3),0)--(sqrt(3),1)--(3-sqrt(3),3-sqrt(3))--(1,sqrt(3))--(0,sqrt(3))--(sqrt(3)-2,3-sqrt(3))--(1-sqrt(3),1)--(1-sqrt(3),0)--(sqrt(3)-2,sqrt(3)-2)--cycle,linewidth(2)); [/asy]$ $\textbf{(A) } -12 \qquad \textbf{(B) }-4 \qquad \textbf{(C) } 4 \qquad \textbf{(D) }24 \qquad \textbf{(E) }32$

Solution 1 (Coord bash)

$[asy] import geometry; unitsize(3cm); draw((0,0) -- (1,0) -- (1,1) -- (0,1) -- cycle); draw(shift((1/2,1-sqrt(3)/2))*polygon(6)); draw(shift((1/2,sqrt(3)/2))*polygon(6)); draw(shift((sqrt(3)/2,1/2))*rotate(90)*polygon(6)); draw(shift((1-sqrt(3)/2,1/2))*rotate(90)*polygon(6)); draw((0,1-sqrt(3))--(1,1-sqrt(3))--(3-sqrt(3),sqrt(3)-2)--(sqrt(3),0)--(sqrt(3),1)--(3-sqrt(3),3-sqrt(3))--(1,sqrt(3))--(0,sqrt(3))--(sqrt(3)-2,3-sqrt(3))--(1-sqrt(3),1)--(1-sqrt(3),0)--(sqrt(3)-2,sqrt(3)-2)--cycle,linewidth(1.5)); draw((3-sqrt(3),3-sqrt(3)) -- (3-sqrt(3),sqrt(3)-2) -- (sqrt(3)-2,sqrt(3)-2) -- (sqrt(3)-2,3-sqrt(3)) -- cycle,linewidth(1.5)); label("$O (0, 0)$",(0.5,0.5),S); dot((0.5,0.5)); label("$A$", (3-sqrt(3), 3-sqrt(3)), NE); label("$B$", (sqrt(3) - 2, 3-sqrt(3)), NW); label("$M$", (0, sqrt(3)), NW); label("$N$", (1, sqrt(3)), NE); [/asy]$

Refer to the diagram above.

Let the origin be at the center of the square, $A$ be the intersection of the top and right hexagons, $B$ be the intersection of the top and left hexagons, and $M$ and $N$ be the top points in the diagram.

By symmetry, $A$ lies on the line $y = x$ . The equation of line $AN$ is $y = -x\sqrt{3} + \frac{3}{2}\sqrt{3} - \frac{1}{2}$ (due to it being one of the sides of the top hexagon). Thus, we can solve for the coordinates of $A$ by finding the intersection of the two lines: $x = -x\sqrt{3} + \frac{3\sqrt{3} - 1}{2}$ $x(\sqrt{3} + 1) = \frac{3\sqrt{3} - 1}{2}$ $x = \frac{3\sqrt{3}-1}{2} \cdot \frac{1}{\sqrt{3} + 1}$ $= \frac{3\sqrt{3}-1}{2(\sqrt{3} + 1)} \cdot \frac{\sqrt{3} - 1}{\sqrt{3} - 1}$ $= \frac{10 - 4\sqrt{3}}{4}$ $= \frac{5}{2} - \sqrt{3}$ $\therefore A = \left(\frac{5}{2} - \sqrt{3}, \frac{5}{2} - \sqrt{3}\right).$

This means that we can find the length $AB$ , which is equal to $2(\frac{5}{2} - \sqrt{3}) = (5 - 2\sqrt{3}$ . We will next find the area of trapezoid $ABMN$ . The lengths of the bases are $1$ and $5 - 2\sqrt{3}$ , and the height is equal to the $y$ -coordinate of $M$ minus the $y$ -coordinate of $A$ . The height of the hexagon is $\sqrt{3}$ and the bottom of the hexagon lies on the line $y = \frac{1}{2}$ . Thus, the $y$ -coordinate of $M$ is $\sqrt{3} - \frac{1}{2}$ , and the height is $2\sqrt{3} - 3$ . We can now find the area of the trapezoid: $[ABMN] = (2\sqrt{3} - 3)\left(\frac{1 + 5 - 2\sqrt{3}}{2}\right)$ $= (2\sqrt{3} - 3)(3 - \sqrt{3})$ $= 6\sqrt{3} + 3\sqrt{3} - 9 - 6$ $= 9\sqrt{3} - 15.$

The total area of the figure is the area of a square with side length $AB$ plus four times the area of this trapezoid: $\textrm{Area} = (5 - 2\sqrt{3})^2 + 4(9\sqrt{3} - 15)$ $= 37 - 20\sqrt{3} + 36\sqrt{3} - 60$ $= 16\sqrt{3} - 23.$

Our answer is $16 + 3 - 23 = \boxed{\textbf{(B) }-4}$ .

~mathboy100

Solution 2

$[asy] import geometry; unitsize(3cm); draw((0,0) -- (1,0) -- (1,1) -- (0,1) -- cycle); draw(shift((1/2,1-sqrt(3)/2))*polygon(6)); draw(shift((1/2,sqrt(3)/2))*polygon(6)); draw(shift((sqrt(3)/2,1/2))*rotate(90)*polygon(6)); draw(shift((1-sqrt(3)/2,1/2))*rotate(90)*polygon(6)); draw((0,1-sqrt(3))--(1,1-sqrt(3))--(3-sqrt(3),sqrt(3)-2)--(sqrt(3),0)--(sqrt(3),1)--(3-sqrt(3),3-sqrt(3))--(1,sqrt(3))--(0,sqrt(3))--(sqrt(3)-2,3-sqrt(3))--(1-sqrt(3),1)--(1-sqrt(3),0)--(sqrt(3)-2,sqrt(3)-2)--cycle,linewidth(2)); draw((0.5,sqrt(3))--(0.5,1-sqrt(3)),linewidth(2)); draw((1-sqrt(3),0.5)--(sqrt(3),0.5),linewidth(2)); draw((-2+sqrt(3),-2+sqrt(3))--(3-sqrt(3),3-sqrt(3)),linewidth(2)); draw((1, sqrt(3))--(1,1),linewidth(2)); label("$O$",(0.5,0.5),SE); dot((0.5,0.5)); label("$A$", (3-sqrt(3), 3-sqrt(3)), NE); label("$B$", (1, sqrt(3)), NE); label("$C$", (1,1), E); label("$D$", (1/2, sqrt(3)), N); [/asy]$

Begin by dividing the figure as shown above. Clearly, the entire figure has 8-fold symmetry. Therefore, we can calculate the area of $ODBA$ and multiply it by 8. We split $[ODBA]$ into $[ODBC]+[ABC]$ .

Knowing the side length of the hexagon is $1$ , we can use 30-60-90 triangles within the hexagon to find the total distance between opposite edges is $2\cdot \frac{\sqrt{3}}{2}=\sqrt{3}.$ Thus, $OD=\sqrt{3}-\frac{1}{2}$ and $BC=\sqrt{3}-1.$ Recognizing $DB=\frac{1}{2}$ and $ODBC$ is a trapezoid, $8\cdot[ODBC]=2\left(\sqrt{3}-\frac{1}{2}+\sqrt{3}-1\right)=4\sqrt{3}-3.$

Next, we aim to find $[ABC]$ . By angle chasing, we find $\angle A=105^\circ,$ $\angle B=30^\circ,$ and $\angle C = 45^\circ.$ We can use the law of sines to find $AB$ :

$\frac{\sin(105^\circ)}{\sqrt{3}-1}=\frac{\sin(45^\circ)}{AB}\implies AB=\frac{\sqrt{6}-\sqrt{2}}{2\sin(105^\circ)}.$

We may not know what $\sin(105^\circ)$ is by memory, but we can cleverly calculate it using a common trig identity:

$\begin{align*} \sin(105^\circ)&=\sin(60^\circ+45^\circ),\\ &=\sin(60^\circ)\cos(45^\circ)+\cos(60^\circ)\sin(45^\circ),\\ &=\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{2}}{2}+\frac{1}{2}\cdot\frac{\sqrt{2}}{2},\\ &=\frac{\sqrt{6}+\sqrt{2}}{4}. \end{align*}$

With some simplification, we'll find $AB=4-2\sqrt{3}$ . Now, we can easily calculate $8\cdot [ABC]$ as $8\cdot\frac{1}{2}\cdot(\sqrt{3}-1)(4-2\sqrt{3})\sin(30^\circ)=12\sqrt{3}-20.$

Thus, the area of the dodecagon is $8\cdot [ODBA] = 8\cdot [ODBC] + 8 \cdot [ABC] =4\sqrt{3}-3+12\sqrt{3}-20=16\sqrt{3}-23.$

Finally, we find $16+3-23=\boxed{\textbf{(B)}\ -4}.$

~Indiiiigo

Solution 3

We calculate the area as the area of the red octagon minus the four purple congruent triangles: $[asy] import geometry; unitsize(3cm); draw((1-sqrt(3),1-sqrt(3))--(1-sqrt(3),sqrt(3))--(sqrt(3),sqrt(3))--(sqrt(3),1-sqrt(3))--cycle,dashed); filldraw((0,1-sqrt(3))--(1,1-sqrt(3))--(sqrt(3),0)--(sqrt(3),1)--(1,sqrt(3))--(0,sqrt(3))--(1-sqrt(3),1)--(1-sqrt(3),0)--cycle,red*0.2+white,red); filldraw((1,1-sqrt(3))--(3-sqrt(3),sqrt(3)-2)--(sqrt(3),0)--cycle,purple*0.2+white,blue); filldraw((sqrt(3),1)--(3-sqrt(3),3-sqrt(3))--(1,sqrt(3))--cycle,purple*0.2+white,blue); filldraw((0,sqrt(3))--(sqrt(3)-2,3-sqrt(3))--(1-sqrt(3),1)--cycle,purple*0.2+white,blue); filldraw((0,1-sqrt(3))--(1-sqrt(3),0)--(sqrt(3)-2,sqrt(3)-2)--cycle,purple*0.2+white,blue); draw((0,0) -- (1,0) -- (1,1) -- (0,1) -- cycle); draw(shift((1/2,1-sqrt(3)/2))*polygon(6)); draw(shift((1/2,sqrt(3)/2))*polygon(6)); draw(shift((sqrt(3)/2,1/2))*rotate(90)*polygon(6)); draw(shift((1-sqrt(3)/2,1/2))*rotate(90)*polygon(6)); [/asy]$ We first find the important angles in the figure. We note that 2 adjacent hexagons are rotated $90^\circ$ with respect to the other, so the angles between any sides is $150^\circ$ . In particular, as the purple triangles are isosceles, they have angles $150^\circ,15^\circ$ , and $15^\circ$ , and the octagon is equiangular (all its angles are $135^\circ$ ). Thus, we can draw a square around the octagon, and we note that the ``cut out" triangles are all isosceles right triangles.

Now, we calculate the side length of the square. Note that the hexagon has a height of $\sqrt 3$ , so the length of a side of the square is $2\sqrt 3-1$ . In particular, the horizontal/vertical sides of the octagon have length $1$ , so the legs of the isosceles triangles are $\frac{2\sqrt3-1-1}2=\sqrt3-1$ Thus, the area of the octagon is $(2\sqrt3-1)^2-4\cdot\frac 12(\sqrt3-1)^2=5$ Now, we calculate the area of one of the four isosceles triangles. The base of the triangle is $(\sqrt 3-1)\sqrt 2$ , so the area is $\frac 14\mathrm{base length}^2\cdot\tan(\mathrm{base angle})=\frac 14((\sqrt3-1)\sqrt2)^2\cdot\tan15^\circ=\frac 14(8-4\sqrt3)(2-\sqrt3)=7-4\sqrt 3$ Thus, the area of the dodecagon is $5-4(7-4\sqrt3)=16\sqrt3-23$ Thus the answer is $16+3-23=-4$ , or $\boxed{\textbf{(B)}}$ .

~cr. naman12

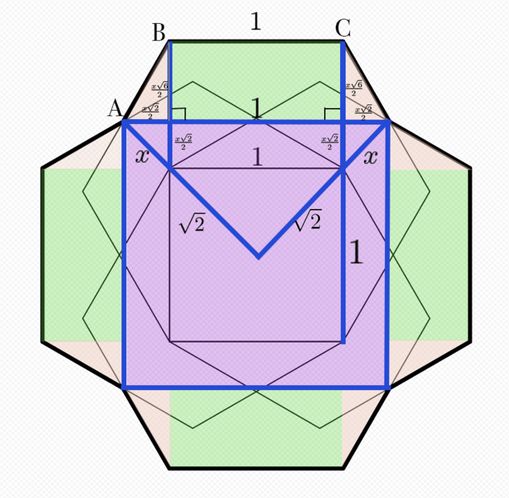
Solution 4

Note that each of the green sections is a rectangle, so its interior angles are all $90^{\circ}.$ Since $\angle{ABC}=120^{\circ}$ , every one of the orange sections is a $30-60-90$ right triangle.

Define $x$ to be the distance from the corner of the square with side length $1$ to the corner of the larger blue square. Due to the sides of the two squares being parallel to each other, the large blue triangle is a $45-45-90$ right triangle. By $AAA$ similarity, the smaller blue triangles are also $45-45-90,$ and have side lengths of $\frac{x\sqrt{2}}{2}, \frac{x\sqrt{2}}{2},$ and $x$ . By $30-60-90$ triangle relations, the largest altitude of the orange triangle is $x\sqrt{6}{2}.$

The height of a hexagon of side length $1$ is $\sqrt{3},$ by the law of cosines. This is also equal to the sum of the values along the long blue line. Therefore, $1+\frac{x\sqrt{2}}{2}+\frac{x\sqrt{6}}{2}=\sqrt{3}.$ Solving and rationalizing, $x=2\sqrt{2}-\sqrt{6}.$

The area of the dodecagon is equal to the sum of the areas of the four rectangles, eight orange triangles, and purple square. In terms of $x$ , this is $8\cdot \frac{1}{2}\cdot \frac{x\sqrt{2}}{2}\cdot \frac{x\sqrt{6}}{{2}}+4\cdot 1\cdot\frac{x\sqrt{6}}{2}+(x\sqrt{2}+1)^2.$

Plugging in $x=2\sqrt{2}-\sqrt{6}$ , the area of the dodecagon is $16\sqrt{3}-23$ . Therefore, the answer is $16+3-12=$ $\boxed{\textbf{(B) }-4}.$

-Benedict T (countmath1)

Video Solution

https://youtu.be/QYclqXWnxxE

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Video Solution by the Power of Logic

https://youtu.be/XBLrFzI3png

2022 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 24	Followed by Last problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search