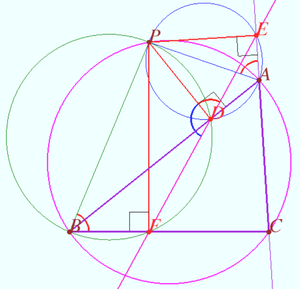
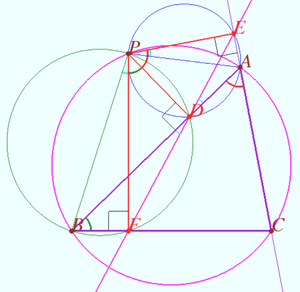
Simson line
In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear.
Proof
In the shown diagram, we draw additional lines ![]() and
and ![]() . Then, we have cyclic quadrilaterals
. Then, we have cyclic quadrilaterals ![]() ,
, ![]() , and
, and ![]() . (more will be added)
. (more will be added)
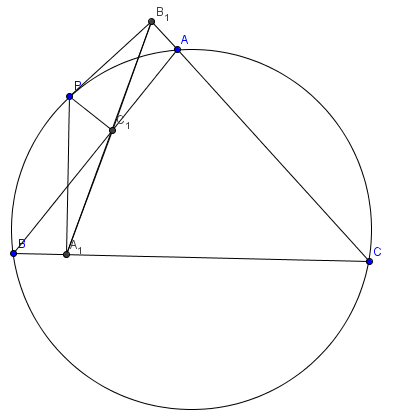
Simson line (main)
Let a triangle ![]() and a point
and a point ![]() be given. Let
be given. Let ![]() and
and ![]() be the foots of the perpendiculars dropped from P to lines AB, AC, and BC, respectively.
be the foots of the perpendiculars dropped from P to lines AB, AC, and BC, respectively.
Then points ![]() and
and ![]() are collinear iff the point
are collinear iff the point ![]() lies on circumcircle of
lies on circumcircle of ![]()
Proof
Let the point ![]() be on the circumcircle of
be on the circumcircle of ![]()
![]()
![]() is cyclic
is cyclic ![]()
![]()
![]() is cyclic
is cyclic ![]()
![]() is cyclic
is cyclic ![]()
![]() and
and ![]() are collinear as desired.
are collinear as desired.
Proof
Let the points ![]() and
and ![]() be collinear.
be collinear.
![]() is cyclic
is cyclic ![]()
![]() is cyclic
is cyclic ![]()
![]()
![]()
![]() is cyclis as desired.
is cyclis as desired.
vladimir.shelomovskii@gmail.com, vvsss