1987 AIME Problems/Problem 15

Problem

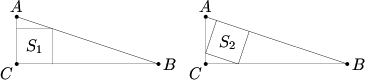
Squares $S_1$ and $S_2$ are inscribed in right triangle $ABC$ , as shown in the figures below. Find $AC + CB$ if area $(S_1) = 441$ and area $(S_2) = 440$ .

Solution

An image is supposed to go here. You can help us out by creating one and editing it in. Thanks.

Because all the triangles in the figure are similar to triangle $ABC$ , it's a good idea to use area ratios. In the diagram above, $\frac {T_1}{T_3} = \frac {T_2}{T_4} = \frac {441}{440}.$ Hence, $T_3 = \frac {440}{441}T_1$ and $T_4 = \frac {440}{441}T_2$ . Additionally, the area of triangle $ABC$ is equal to both $T_1 + T_2 + 441$ and $T_3 + T_4 + T_5 + 440.$

Setting the equations equal and solving for $T_5$ , $T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}$ . Therefore, $441T_5 = 441 + T_1 + T_2$ . However, $441 + T_1 + T_2$ is equal to the area of triangle $ABC$ ! This means that the ratio between the areas $T_5$ and $ABC$ is $441$ , and the ratio between the sides is $\sqrt {441} = 21$ . As a result, $AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}$ . We now need $(AC)(BC)$ to find the value of $AC + BC$ , because $AB^2 + 2(AC)(BC) = (AC + BC)^2$ .

Let $h$ denote the height to the hypotenuse of triangle $ABC$ . Notice that $h - \frac {1}{21}h = \sqrt {440}$ . (The height of $ABC$ decreased by the corresponding height of $T_5$ ) Thus, $(AB)(h) = (AC)(BC) = 22\cdot 21^2$ . Because $AB^2 + 2(AB)(BC) = (AC + BC)^2 = 21^2\cdot22^2$ , $AC + BC = (21)(22) = 462$ .[/

1987 AIME (Problems • Answer Key • Resources)
Preceded by Problem 14	Followed by Last Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

1987 AIME Problems/Problem 15

Problem

Solution

See also