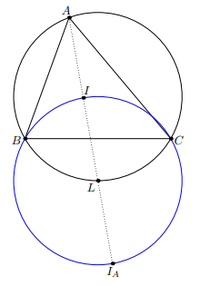
Incenter/excenter lemma
In geometry, the incenter/excenter lemma, sometimes called the Trillium theorem, is a result concerning a relationship between the incenter and excenter of a triangle. Given a triangle ![]() with incenter
with incenter ![]() and
and ![]() -excenter
-excenter ![]() , let
, let ![]() be the midpoint of the arc
be the midpoint of the arc ![]() of the triangle's circumcenter. Then, the theorem states that
of the triangle's circumcenter. Then, the theorem states that ![]() is the center of a circle through
is the center of a circle through ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
The incenter/excenter lemma makes frequent appearances in olympiad geometry. Along with the larger lemma, two smaller results follow: first, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are collinear, and second,
are collinear, and second, ![]() is the reflection of
is the reflection of ![]() across
across ![]() . Both of these follow easily from the main proof.
. Both of these follow easily from the main proof.
Proof
Let ![]() ,
, ![]() ,
, ![]() ,
and note that
,
and note that ![]() ,
, ![]() ,
, ![]() are collinear (as
are collinear (as ![]() is on the angle bisector).
We are going to show that
is on the angle bisector).
We are going to show that ![]() , the other cases being similar.
, the other cases being similar.
First, notice that
\angle LBI = \angle LBC + \angle CBI
= \angle LAC + \angle CBI
= \angle IAC + \angle CBI
= \half A + \half B.
However,
\angle BIL = \angle BAI + \angle ABI
= \half A + \half B.
Hence, ![]() is isosceles.
So
is isosceles.
So ![]() .
The rest of the proof proceeds along these lines.
.
The rest of the proof proceeds along these lines.