2019 AMC 8 Problems/Problem 12

Problem

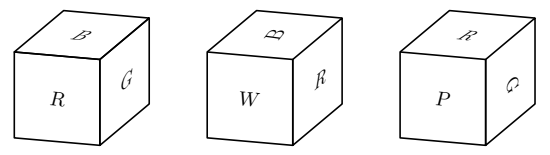
The faces of a cube are painted in six different colors: red (R), white (W), green (G), brown (B), aqua (A), and purple (P). Three views of the cube are shown below. What is the color of the face opposite the aqua face?

$\textbf{(A) }\text{red}\qquad\textbf{(B) }\text{white}\qquad\textbf{(C) }\text{green}\qquad\textbf{(D) }\text{brown}\qquad\textbf{(E) }\text{purple}$

Solution 1

$B$ is on the top, and $R$ is on the side, and $G$ is on the right side. That means that (image 2) $W$ is on the left side. From the third image, you know that $P$ must be on the bottom since $G$ is sideways. That leaves us with the back, so the back must be $A$ . The front is opposite of the back, so the answer is $\boxed{\textbf{(A)}\ R}$ .~heeeeeeeheeeee

Solution 2

Looking closely we can see that all faces except for $A$ are connected with $R$ . Thus the answer is $\boxed{\textbf{(A)}\ R}$ .

~phoenixfire

Note

2019 AMC 8 (Problems • Answer Key • Resources)
Preceded by Problem 11	Followed by Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

Only two of the cubes are required to solve the problem.

Page

Toolbox

Search

2019 AMC 8 Problems/Problem 12

Contents

Problem

Solution 1

Solution 2

Note