2001 AIME I Problems/Problem 6

Problem

A fair die is rolled four times. The probability that each of the final three rolls is at least as large as the roll preceding it may be expressed in the form $\frac{m}{n}$ where $m$ and $n$ are relatively prime positive integers. Find $m + n$ .

Solutions

Solution 1

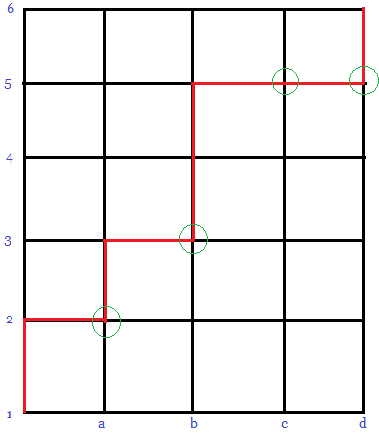
Recast the problem entirely as a block-walking problem. Call the respective dice $a, b, c, d$ . In the diagram below, the lowest $y$ -coordinate at each of $a$ , $b$ , $c$ , and $d$ corresponds to the value of the roll.

The red path corresponds to the sequence of rolls $2, 3, 5, 5$ . This establishes a one-to-one correspondence between valid dice roll sequences and block walking paths.

The solution to this problem is therefore $\dfrac{\binom{9}{4}}{6^4} = {\dfrac{7}{72}}$ . So the answer is $\boxed{79}$ .

Solution 2

If we take any combination of four numbers, there is only one way to order them in a non-decreasing order. It suffices now to find the number of combinations for four numbers from $\{1,2,3,4,5,6\}$ . We can visualize this as taking the four dice and splitting them into 6 slots (each slot representing one of {1,2,3,4,5,6}), or dividing them amongst 5 separators. Thus, there are ${9\choose4} = 126$ outcomes of four dice. The solution is therefore $\frac{126}{6^4} = \frac{7}{72}$ , and $7 + 72 = \boxed{079}$ .

Solution 3

Call the dice rolls $a, b, c, d$ . The difference between the $a$ and $d$ distinguishes the number of possible rolls there are.

If $a - d = 0$ , then the values of $b,\ c$ are set, and so there are $6$ values for $a,\ d$ .
If $a - d = 1$ , then there are ${3\choose2} = 3$ ways to arrange for values of $b,\ c$ , but only $5$ values for $a,\ d$ .
If $a - d = 2$ , then there are ${4\choose2} = 6$ ways to arrange $b, c$ , and there are only $6 - 2 = 4$ values for $a, d$ .

Continuing, we see that the sum is equal to $\sum_{i = 0}^{5}{i+2\choose2}(6 - i) = 6 + 15 + 24 + 30 + 30 + 21 = 126$ . The requested probability is $\frac{126}{6^4} = \frac{7}{72}$ .

Solution 4

The dice rolls can be in the form

ABCD
AABC
AABB
AAAB
AAAA

where A, B, C, D are some possible value of the dice rolls. (These forms are not keeping track of whether or not the dice are in ascending order, just the possible outcomes.)

Now, for the first case, there are ${6\choose4} = 15$ ways for this. We do not have to consider the order because the combination counts only one of the permutations; we can say that it counts the correct (ascending order) permutation.
Second case: ${6\choose3} = 20$ ways to pick 3 numbers, ${3\choose1}$ ways to pick 1 of those 3 to duplicate. A total of 60 for this case.
Third case: ${6\choose2}=15$ ways to pick 2 numbers. We will duplicate both, so nothing else in this case matters.
Fourth case: ${6\choose2} = 15$ ways to pick 2 numbers. We pick one to duplicate with ${2\choose1} = 2$ , so there are a total of 30 in this case.
Fifth case: ${6\choose1} = 6$ ; all get duplicated so nothing else matters.

There are a total of $6^4$ possible dice rolls.

Thus,

$\frac{m}{n} = \frac{15 + 60 + 15 + 30 + 6}{6^4} = \frac{126}{6^4} = \frac{7}{72}$

Solution 5

Consider the number of possible dice roll combinations which work after $1$ roll, after $2$ rolls, and so on. There is 6 possible rolls for the first dice. If the number rolled is a 1, then there are 6 further values that are possible for the second dice; if the number rolled is a 2, then there are 5 further values that are possible for the second dice, and so on.

Suppose we generalize this as a function, say $f(l,r)$ return the number of possible combinations after $l$ rolls and $r$ being the beginning value of the first roll. It becomes clear that from above, $f(1,r) = 1$ ; every value of $l$ after that is equal to the sum of the number of combinations of $l - 1$ rolls that have a starting value of at least $r$ . If we slowly count through and add up all the possible combinations we get $\frac{7}{72}$ possibilities.

Solution 6

In a manner similar to the above solution, instead consider breaking it down into two sets of two dice rolls. The first subset must have a maximum value which is $\le$ the minimum value of the second subset.

If the first subset ends in a 1, there is $1$ such subset and there are $6 + 5 + 4 + 3 + 2 + 1 = \frac{6}{2}(6 + 1) = 21$ ways of making the second subset.
If the first subset ends in a 2, there is $2$ such subsets and there are $5 + \ldots + 1 = \frac{5}{2}(5 + 1) = 15$ ways of making the second subset.

Thus, the number of combinations is $\sum_{i=1}^6 i \cdot \left(\frac{(7 - i)(8 - i)}{2}\right) = 21 + 30 + 30 + 24 + 15 + 6 = 126$ , and the probability again is $\frac7{72}$ .

Solution 7 Recursion formula for the brain dead

If you're too tired to think about any of the above smart transformations of the problem, a recursion formula can be a robust way to the correct answer.

We just need to work out the valid cases for each roll. Denote by $N_{k}(n)$ the number of valid cases in the $k+1$ -th roll when the number $n$ is rolled, for $k=1,2,3$ and $1 <= n <= 6$ . Then we have the following recursion formula: $N_{1}(n) = n$ $N_{2}(n) = N_{1}(1) + N_{1}(2) + ... + N_{1}(n)=N_{2}(n-1)+N_{1}(n)$ $N_{3}(n) = N_{2}(1) + N_{2}(2) + ... + N_{2}(n)=N_{3}(n-1)+N_{2}(n)$ The logic is that, if $n$ is rolled, then the number of valid cases is the subtotal of valid cases in the preceding roll for the outcome of 1 to $n$ . The recursion can be easily calculated by hand when $N_k(n)$ are put in columns side by side, given the fact that te numbers are smaller than 100. Finally, the total number of cases is $N = \sum_{n=1}^{6} N_{3}(n)$ and $P = \frac{N}{6^4}$

Solution 8

Lets try casework and observe the cases. Notice that if the last roll is a $1$ , then the only dice rolls may be $1-1-1-1$ , which is only $1$ possibility. Observe that if the last roll is $2$ , then there are $4$ possibilities. When the last roll is a $3$ , there are $10$ possibilities. Notice when the last roll is $n$ , it is the sum of the first $n$ positive triangular numbers. So there are a total of $1 + 1 + 3 + 1 + 3 + 6 + 1 + 3 + 6 + 10 + 1 + 3 + 6 + 10 + 15 + 1 + 3 + 6 + 10 + 15 + 21 = 126$ possibilities. So the probability is $\frac{126}{6^4} = \frac{7}{72}$ so $7 + 72 = \boxed{079}$ . ~skyscraper

2001 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 5	Followed by Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search