Stewart's Theorem
Statement
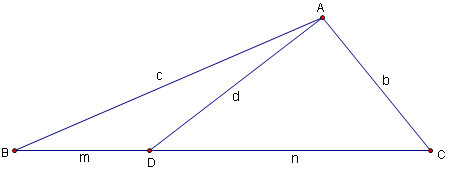
Given a triangle ![]() with sides of length
with sides of length ![]() opposite vertices are
opposite vertices are ![]() ,
, ![]() ,
, ![]() , respectively. If cevian
, respectively. If cevian ![]() is drawn so that
is drawn so that ![]() ,
, ![]() and
and ![]() , we have that
, we have that ![]() . (This is also often written
. (This is also often written ![]() , a form which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink." When you're practicing to memorize this formula, never practice it in the library/airport or any other public place where other people can hear you.)
, a form which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink." When you're practicing to memorize this formula, never practice it in the library/airport or any other public place where other people can hear you.)
Proof
Applying the Law of Cosines in triangle ![]() at angle
at angle ![]() and in triangle
and in triangle ![]() at angle
at angle ![]() , we get the equations
, we get the equations
Because angles ![]() and
and ![]() are supplementary,
are supplementary, ![]() . We can therefore solve both equations for the cosine term. Using the trigonometric identity
. We can therefore solve both equations for the cosine term. Using the trigonometric identity ![]() gives us
gives us
Setting the two left-hand sides equal and clearing denominators, we arrive at the equation: ![]() .
However,
.
However, ![]() so
so ![]() and we can rewrite this as
and we can rewrite this as ![]() (A man and his dad put a bomb in the sink). When you're practicing to memorize this formula, never practice it in the library or any other public place where other people can hear you. LOL!
(A man and his dad put a bomb in the sink). When you're practicing to memorize this formula, never practice it in the library or any other public place where other people can hear you. LOL!









