Barycentric coordinates

This can be used in mass points. http://mathworld.wolfram.com/BarycentricCoordinates.html This article is a stub. Help us out by expanding it.

Barycentric coordinates are triples of numbers $(t_1,t_2,t_3)$ corresponding to masses placed at the vertices of a reference triangle $\Delta{A_1}{A_2}{A_3}$ . These masses then determine a point $P$ , which is the geometric centroid of the three masses and is identified with coordinates $(t_1,t_2,t_3)$ . The vertices of the triangle are given by $(1,0,0)$ , $(0,1,0)$ , and $(0,0,1)$ . Barycentric coordinates were discovered by Möbius in 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).

The Central NC Math Group published a lecture concerning this topic at https://www.youtube.com/watch?v=KQim7-wrwL0 if you would like to view it.

1 Useful formulas
2 Product of isogonal segments
3 Ratio of isogonal segments
4 Point on incircle
5 Crossing point
6 Fixed point on circumcircle
7 Two pare isogonal points
8 Collinearity for two pares of isogonal points
9 Points on bisectors
10 Crosspoint of median and set of secants
11 Set of lines in triangle
12 Set of parallel lines
13 Feuerbach point of a scalene triangle
14 Small Pascal's theorem

Useful formulas

Notation

Let the triangle $\triangle ABC$ be a given triangle, $a, b, c,$ be the lengths of $BC, AC, AB, \angle A = \alpha, \angle B = \beta, \angle C = \gamma.$

We use the following Conway symbols:

$s = \frac {a+b+c}{2}$ is semiperimeter, $2S$ is twice the area of $\triangle ABC,$

$r^2 = \frac {(s-a)(s-b)(s-c)}{s},$ where $r$ is the inradius, $R = \frac {abc}{2 \cdot 2S}$ is the circumradius,

$\cos \omega = \frac {a^2 + b^2 +c^2}{2 \cdot 2S}$ is the cosine of the Brocard angle,

$S_A = bc \cos \alpha = \frac{b^2+c^2-a^2}{2}, S_B = ac \cos \beta =\frac{a^2 +c^2-b^2}{2}, S_C = ab \cos \gamma = \frac {a^2+b^2-c^2}{2}.$

Main

For any point in the plane $ABC$ there are barycentric coordinates(BC): $\vec X = (x_X : y_X : z_X)$ $x_X \cdot \vec {XA} + y_X \cdot \vec {XB} + z_X \cdot \vec {XC} = \vec {0},$ $\vec X = \frac {x_X \cdot \vec {A} + y_X \cdot \vec {B} + z_X \cdot \vec {C}}{x_X + y_X + z_X}.$ The normalized (absolute) barycentric coordinates NBC satisfy the condition $x_X + y_X + z_X = 1,$ they are uniquely determined: $x_X = \frac{[\vec {XB},\vec {XC}]}{\sigma}, y_X = \frac{[\vec {XC},\vec {XA}]}{\sigma}, z_X = \frac{[\vec {XA},\vec {XB}]}{\sigma},$ $\sigma = [\vec {XB},\vec {XC}] + [\vec {XC},\vec {XA}] + [\vec {XA},\vec {XB}] .$ Triangle vertices $A = (1:0:0), B = (0:1:0), C = (0:0:1).$

The barycentric coordinates of a point do not change under an affine transformation.

Lines

The straight line in barycentric coordinates (BC) is given by the equation $kx + ly + mz = 0.$

The lines given in the BC by the equations $k_1x + l_1y + m_1z = 0$ and $k_2x + l_2y + m_2z = 0$ intersect at the point $(l_1m_2 – m_1l_2 : m_1k_2-k_1m_2 : k_1l_2-l_1k_2).$

These lines are parallel iff $l_1m_2 – m_1l_2 + m_1k_2-k_1m_2 + k_1l_2-l_1k_2 = 0.$

The sideline $BC$ contains the points $B = (0:1:0), C = (0:0:1),$ its equation is $x = 0.$

The line $AX, X = (k : l : m)$ has equation $l z = m y,$ it intersects the sideline $BC$ at the point $A_X = (0 : l : m), \frac {BA_X}{A_XC} = \frac {m}{l}, \frac {AX}{XA_X} = \frac {m + l}{k}.$

Iff $A_X = (0 : l : m), B_X = (k : 0 : m ), C_X = (k : l : 0),$ then $AA_X \cap BB_X \cap CC_X = (k : l : m ).$

Let NBC of points $P$ and $Q$ be $P = (x_1 : y_1 : z_1), Q = (x_2 : y_2 : z_2).$

Then the square of distance $|PQ|^2 = S_A \cdot (x_1 - x_2)^2 + S_B \cdot (y_1 - y_2)^2 + S_C \cdot (z_1 - z_2)^2.$ $|PQ|^2 = - a^2 (y_1 - y_2)(z_1 - z_2) - b^2 (x_1 - x_2)(z_1 - z_2) - c^2 (x_1 - x_2)(y_1 - y_2).$ The equation of bisector of $PQ$ is: $x(c^2(y_2-y_1) + b^2(z_2-z_1)) + y(a^2(z_2-z_1) + c^2(x_2-x_1)) + z(a^2(y_2-y_1) + b^2(x_2-x_1)) + a^2(y_1z_1 - y_2z_2) + b^2(x_1z_1-x_2z_2) + c^2 (x_1y_1 – x_2y_2) =0.$ Nagel line : $(b-c) x + (c-a) y + (a-b) z = 0.$

Circles

Any circle is given by an equation of the form $(kx + ly + mz)(x +y + z) = xyc^2 + xzb^2 + yza^2.$

Circumcircle contains the points $A = (1:0:0), B = (0:1:0), C = (0:0:1) \implies$ the equation of this circle: $xyc^2 + xzb^2 + yza^2 = 0.$

The incircle contains the tangent points of the incircle with the sides: $\left(0 : \frac {a+b-c}{2a} : \frac {a-b+c}{2a}\right), \left(\frac {a+b-c}{2b} : 0 : \frac {-a+b+c}{2b}\right), \left(\frac {a-b+c}{2c} : \frac {-a+b+c}{2c} : 0\right).$

The equation of the incircle is ${k_a}^2x^2 + k_b^2y^2 + k_c^2z^2 - 2k_a k_b xy - 2k_a k_c xz - 2k_bk_cyz = 0,$ where $k_a = b+c - a, k_b = a+c - b, k_c = a + b - c.$

The radical axis of two circles given by equations of this form is: $(k_1 - k_2) a \cdot x + (l_1 - l_2) b \cdot y + (m_1 - m_2) c \cdot z = 0.$ Conjugate

The point $P = (x : y : z)$ is isotomically conjugate with respect to $\triangle ABC$ with the point $P_1 =\left( \frac {1}{x} : \frac {1}{y} : \frac {1}{z}\right).$

The point $P = (x : y : z)$ is isogonally conjugate with respect to $\triangle ABC$ with the point $P_2 =\left( \frac {a^2}{x} : \frac {b^2}{y} : \frac {c^2}{z}\right).$

The point $P = (x : y : z)$ is isocircular conjugate with respect to $\triangle ABC$ with the point $P_3 = \left(\frac {x}{a} : \frac {y}{b} : \frac {z}{c}\right).$

Triangle centers

The median $AA_G, A_G \in BC \implies \frac {BA_G}{CA_G} = 1 \implies$ centroid is $G = (1 : 1 : 1).$

The simmedian point $K$ is isogonally conjugate with respect to $\triangle ABC$ with the point $G \implies K = \left( a^2 : b^2 : c^2\right).$

The bisector $AA_I, A_I \in BC \implies \frac {BA_I}{CA_I} = \frac {c}{b} \implies$ the incenter is $I = (a : b: c).$

The excenters are $I_A = (-a : b : c), I_B =(a : -b: c), I_C = (a : b : -c).$

The circumcenter $O$ lies at the intersection of the bisectors $AB (c^2(x - y) + z(a^2 - b^2) =0)$ and $AC (b^2(x - z) + y(a^2 - c^2) =0) \implies$ its BC coordinates $O = (a^2S_A : b^2S_B : c^2S_C).$

The orthocenter $H$ is isogonally conjugate with respect to $\triangle ABC$ with the point $O \implies H =\left( \frac {1}{S_A} : \frac {1}{S_B} : \frac {1}{S_C}\right).$

Let Nagel point $N$ lies at line $AA_N, A_N \in BC \implies \frac {BA_N}{A_NC} = \frac {a+c-b}{a+b-c} \implies N=(b+c-a: a+c-b:a+b-c).$

The Gergonne point is the isotomic conjugate of the Nagel point, so $Ge=\left( \frac {1}{b+c-a} : \frac{1}{a+c-b} : \frac{1}{a+b-c}\right ).$

vladimir.shelomovskii@gmail.com, vvsss

Product of isogonal segments

Let triangle $\triangle ABC,$ the circumcircle $\Omega$ and isogonals $AF$ and $AG (F,G \in \Omega)$ of the $\angle BAC$ be given. Let point $P'$ and $Q'$ be the isogonal conjugate of a point $P$ and $Q$ with respect to $\triangle ABC.$ Prove that $PF \cdot P'G = Q'F \cdot QG.$

Proof

We fixed $\triangle ABC$ and the point $F.$ So isogonal $AG$ is fixed.

Denote $D = BC \cap AF, E = BC \cap AG.$

We need to prove that $PF \cdot P'G$ do not depends from $P.$

Line $AP$ has the equation $y_P z = z_P y \implies \frac {BD}{DC} = \frac {z_P}{y_P}.$

To find the point $F$ we solve the equation: $x_F y_P c^2 + x_F z_P b^2 + y_P z_P a^2 = 0.$

$F = (x_F : y_F : z_F) = \left(\frac{- a^2 y_P z_P}{c^2 y_P +b^2 z_P} : y_P : z_P \right).$ We use the formula for isogonal cobnjugate point and get $P' = (x_{P'} : y_{P'} : z_{P'}) = \left(\frac {a^2}{x_P} : \frac {b^2}{y_P} : \frac {c^2}{z_P}\right)$ and then $\frac {BE}{EC} = \frac {c^2 y_P}{b^2 z_P}.$

To find the point $G$ we solve the equation: $x_G \cdot \frac {b^2}{y_P} \cdot c^2 + x_G \cdot \frac {c^2}{z_P} \cdot b^2 + \frac {b^2 c^2}{y_P \cdot z_P} \cdot a^2 = 0.$ $G = (x_G : y_G : z_G) = \left(\frac{- a^2}{y_P + z_P} : \frac {b^2}{y_P} : \frac {c^2}{z_P}\right).$ We calculate distances (using NBC) and get: $PF \cdot P'G = \frac {a^2 bc y_P z_P}{\psi},$ $FG = \frac {a|b^2 z_P^2 - c^2 y_P^2|}{\psi},$ where $\psi$ has sufficiently big formula.

Therefore $\frac {FG\cdot a\cdot c}{b\cdot PF \cdot P'G} = \left|\frac {z_P}{y_P} - \frac {c^2 y_P}{b^2 z_P}\right| = \left|\frac {BD}{DC}- \frac {BE}{EC}\right|. \blacksquare$ vladimir.shelomovskii@gmail.com, vvsss

Ratio of isogonal segments

Let triangle $\triangle ABC$ and point $P$ be given. Denote $P'$ the isogonal conjugate of a point $P$ with respect to $\triangle ABC, \Omega = \odot ABC,$ $D = AP' \cap BC, E = AP \cap BC, L = AP \cap \Omega.$ Prove that $\frac {AP'}{P'D} \cdot \frac {AP}{PE} = \frac {AL}{LE}.$

Proof

We use the formula for isogonal conjugate point and get $P = (x_P : y_P : z_P), P' = (x_{P'} : y_{P'} : z_{P'}) = \left( \frac {a^2}{x_P} : \frac {b^2}{y_P} : \frac {c^2}{z_P} \right).$ $\frac {AP'}{P'D} = \frac {y_{P'} + z_{P'}}{x_{P'}},$ $\frac {AP}{PE} = \frac {y_{P} + z_{P}}{x_{P}}.$ $L \in \Omega \implies x_{L'} + y_{L'} + z_{L'} = 0, L \in AP \implies y_L = y_P, z_L = z_P \implies \frac {a^2}{x_L} + y_{P'} + z_{P'} = 0 \implies x_L = \frac{-a^2}{y_{P'} + z_{P'}}.$ $\frac {AL}{LE} = \frac {y_{P} + z_{P}}{-x_{L}} = \frac {(y_{P} + z_{P})(y_{P'} + z_{P'})}{a^2}.$ $x_P \cdot x_{P'} = a^2 \implies \frac {AP'}{P'D} \cdot \frac {AP}{PE} = \frac {AL}{LE}.$

vladimir.shelomovskii@gmail.com, vvsss

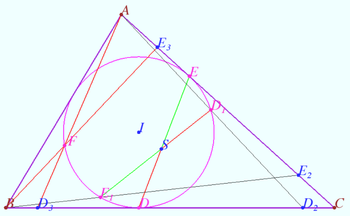
Point on incircle

Let triangle $\triangle ABC$ be given. Denote the incircle $\omega,$ the incenter $I$ , the Spieker center $S, D = \omega \cap BC, E = \omega \cap AC.$

Let $D_1 \in \omega$ be the point corresponding to the condition $SD = SD_1, D_2 = AD_1 \cap BC, D_3$ is symmetric $D_2$ with respect midpoint $BC.$

Symilarly denote $E_3 \in AC.$

Prove that point $F = AD_3 \cap BE_3$ lies on $\omega.$

Proof $I = (a : b : c), S = (b+c : a +c : a+b),$ $D = \left(0 : a+b-c : a-b+c \right), D_1 = (x : y : z ).$ We calculate distances (using NBC) and solve the system of equations: $ID_1^2 = ID^2, SD_1^2 = SD^2.$

We know one solution of this system (point D), so we get linear equation and get: $D_1 = \left((b-c)^2 \cdot (3a-b-c)^2 : (a-b)^2 \cdot(b+c-a)\cdot(-b+a+c) : (a-c)^2\cdot(b+c-a) \cdot(b+a-c) \right) \implies$ $D_2 = \left(0 : (a-b)^2 \cdot(b+c-a) : (b-c)^2 \cdot(b+a-c) \right) \implies$ $D_3 = \left(0 : (b-c)^2 \cdot(b+a-c): (a-b)^2 \cdot(b+c-a) \right) .$ Similarly $E_3 = \left((b-c)^2 \cdot(b+a-c) : 0 : (a-b)^2 \cdot(b+c-a) \right) \implies$ Therefore $F = \left(\frac {(b-c)^2}{b+c-a} : \frac{(a-c)^2}{a+c-b} : \frac{(a-b)^2}{a+b-c}) \right).$ We calculate the length of the segment $FI$ and get $FI^2 = r^2.$

The author learned about the existence of such a point from Leonid Shatunov in August 2023.

vladimir.shelomovskii@gmail.com, vvsss

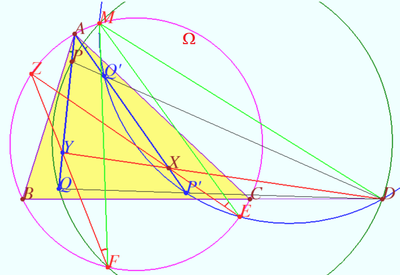
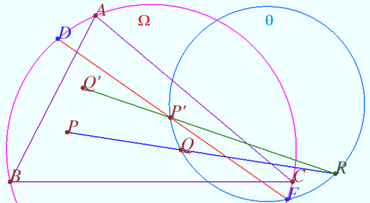
Crossing point

Let triangle $\triangle ABC,$ and points $P$ and $D \in BC$ be given. Let point $P'$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC, \Omega = \odot ABC.$ Let $X$ be an arbitrary point at $AP', Y = DX \cap AP, Q = DP' \cap AP,$ $Q' = DP \cap AP', E = \odot DP'Q' \cap \Omega, F = \odot DPQ \cap \Omega.$ Prove that $EX \cap FY$ lies on $\Omega.$

This configuration can be used as a straight-line mechanism since it allows to create a mechanism that converts the rotational motion of a point Z to perfect straight-line motion of the X point or vice versa. Of course, we need to use the prismatic joint at the points $E$ and $F.$

Proof

We use the barycentric coordinates: $P = (x_P : y_P : z_P), D = (0 : y_D : z_D),$ $X = \left ( x_X : \frac {b^2}{y_P} : \frac {c^2}{z_P} \right), P' = \left (\frac {a^2}{x_P} : \frac {b^2}{y_P} : \frac {c^2}{z_P} \right).$ We get the equations for some lines:

Line $AP$ is $z_P \cdot y - y_P \cdot z = 0,$

line $AP'$ is $c^2 y_P \cdot y - b^2 z_P \cdot z = 0,$

line $DX$ is $\frac {c^2 y_P y_D - b^2 z_P z_D}{x_X y_P z_P} \cdot x + z_D \cdot y - y_D \cdot z = 0,$

line $DP$ is $(z_D y_P - y_D z_P ) \cdot x - z_D x_P \cdot y + y_D x_P \cdot z = 0,$

line $DP'$ is $\left( \frac {b^2 z_D}{y_P}- \frac{c^2 y_D}{z_P}\right) \cdot x - \frac {a^2 z_D}{x_P}\cdot y + \frac{a^2 y_D}{x_P} \cdot z = 0.$

We get the equations for some points:

point $Q$ is $(x_Q : y_Q : z_Q) = \left( \frac {a^2 y_P z_P (z_P y_D - y_P z_D)}{x_P (c^2 y_P y_D - b^2 z_P z_D)} : y_P : z_P \right),$

point $Q'$ is $\left( \frac {a^2}{x_Q} : \frac{b^2}{y_Q} : \frac{c^2}{z_Q} \right),$

point $Y$ is $\left( \frac {x_X y_P z_P ( y_D z_P - y_P z_D)}{c^2 y_D y_P – b^2 z_P z_D} : y_P : z_P \right).$

Any circle is given by an equation of the form $(kx + ly + mz)(x +y + z) = xyc^2 + xzb^2 + yza^2.$ We find the coefficients for the circles (these formulas are big), but can be used for calculations of the crossing points: $E = \left( a^2 : b^2 (\frac {z_P y_D}{y_P z_D} - 1) : c^2 (\frac {y_P z_D}{z_P y_D} - 1 \right),$ $F = \left( a^2 : -b^2 + c^2 \frac {y_P y_D}{z_P z_D} : b^2 \frac {z_P z_D}{y_P y_D} - c^2 \right),$ We get the equations for some lines $EX$ and $FY$ : $(y_D + z_D) \cdot (y_D z_P - y_P z_D)\cdot x + \frac{y_P z_D ((y_P z_D - y_D z_P) x_X + y_D a^2}{b^2}\cdot y + \frac {(y_P z_D - y_D z_P) x_X + a^2 z_D ) z_P y_D}{c^2} \cdot z = 0,$

$(y_D + z_D)(c^2 y_D y_P - b^2 z_D z_P) x + ((y_P z_D - y_D z_P) x_X - y_D a^2) z_D z_P y + y_D y_P(y_P z_D - y_D z_P) x_X + a^2 z_D) z = 0.$ We get the equation for the point $Z$ $\left(\frac {1}{y_D + z_D} : \frac {b^2}{ x_X (y_P z_D - z_P y_D) - a^2 y_D} :\frac {c^2}{x_X (z_P y_D - y_P z_D) - a^2 z_D} \right).$ Let point $Z'$ be the isogonal conjugate of a point $Z$ with respect to a triangle $\triangle ABC.$ $Z' = \left(a^2 (y_D + z_D) : x_X (y_P z_D - z_P y_D) - a^2 y_D : x_X (z_P y_D - y_P z_D) - a^2 z_D \right).$ The sum of coordinates is equal zero, so $Z'$ is in infinity, therefore the point $Z$ lies on $\Omega.\blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

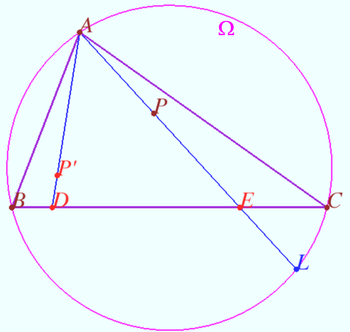
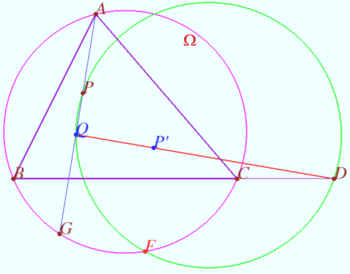
Fixed point on circumcircle

Let triangle $\triangle ABC,$ point $G \ne A$ on circumcircle $\Omega = \odot ABC,$ and point $D \in BC$ be given. Point $P$ lies on $AG,$ point $P'$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC, Q = DP' \cap AP, F = \odot DPQ \cap \Omega.$

Prove that $F$ is fixed point and not depends from position of $P.$

Proof

Denote the coordinates of the points $D = (0 : y_D : z_D), G = (x_G : y_G : z_G).$ $G \in \Omega \implies a^2 y_G z_G + b^2 x_G z_G + c^2 x_G y_G = 0 \implies$ $G = \left( \frac {- a^2 y_G z_G}{b^2 z_G + c^2 y_G} : y_G : z_G\right).$ $P = (x_P : y_G : z_G) \implies P' = \left( \frac {a^2}{x_P} : \frac {b^2}{y_G} : \frac {c^2}{z_G}\right).$ The line $AG$ is $z_G y = y_G z.$

The line $DP'$ is $(y_{P'} z_D - z_{P'} y_D) x - x_{P'} z_D y + x_{P'} y_D z = 0 \implies$ $Q =\left( \frac {a^2 (y_D z_G - y_G z_D) \cdot y_G z_G}{x_P (c^2 y_D y_G - b^2 z_D z_P)} : y_G : z_G \right).$ We find the circle $\odot PQD$ and get the point $F =\left( \frac {a^2}{\frac {c^2}{z_D \cdot z_G} - \frac{b^2}{y_D \cdot y_G}} : y_G \cdot y_D : - z_G \cdot z_D \right).$ $F$ depends only from points $G$ and $D.$

Fixed point on circumcircle

vladimir.shelomovskii@gmail.com, vvsss

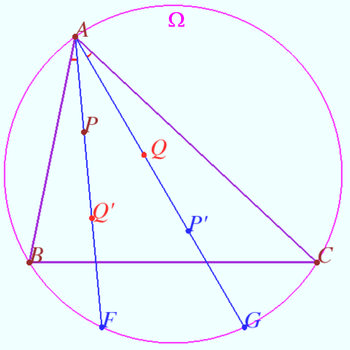
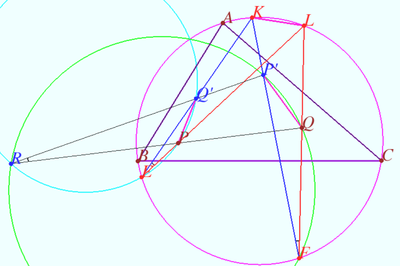
Two pare isogonal points

Let triangle $\triangle ABC,$ and points $P$ and $Q$ (points do not lie on sidelines) be given.

Let point $P'$ and $Q'$ be the isogonal conjugate of a point $P$ and $Q$ with respect to a triangle $\triangle ABC, \Omega = \odot ABC.$

Denote $R = PQ \cap P'Q', E = \Omega \cap RPQ', F = \Omega \cap RQP'.$

Prove that $L= EP \cap FQ$ and $K = EQ' \cap FP'$ lies on $\Omega.$

Proof

The line $PQ$ is $(y_P z_Q - z_P y_Q) x + (x_Q z_P – x_P z_Q) y + (x_P y_Q - x_Q y_P)z = 0.$ The line $P'Q'$ is $(y_P z_Q - z_P y_Q) \frac {x_P x_Q}{a^2} x + (x_Q z_P – x_P z_Q) \frac {y_P y_Q}{b^2}y + (x_P y_Q - x_Q y_P) \frac {z_P z_Q}{c^2}z = 0.$ $R = PQ \cap P'Q' = \left ( a^2 \frac {(b^2 z_P z_Q – c^2 y_P y_Q)}{y_P z_Q – z_P y_Q} : b^2 \frac {(a^2 z_P z_Q – c^2 x_P x_Q)}{x_P z_Q – z_P x_Q} : c^2 \frac {(a^2 y_P y_Q – b^2 x_P x_Q)}{x_P y_Q – y_P x_Q} \right)$ $E = \Omega \cap RPQ' = \left( \frac {a^2}{x_Q (z_P y_Q – y_P z_Q)} : \frac {b^2}{y_Q (x_P z_Q – z_P y_Q)} : \frac {c^2}{z_Q (y_P x_Q – x_P y_Q)} \right).$ $F = \Omega \cap RP'Q = \left( \frac {a^2}{x_P (z_P y_Q – y_P z_Q)} : \frac {b^2}{y_P (x_P z_Q – z_P y_Q)} : \frac {c^2}{z_P (y_P x_Q – x_P y_Q)} \right).$ $K = EQ' \cap FP' = \left( \frac {a^2}{x_Q (y_P + z_P) - x_P (y_Q + z_Q)} : \frac {b^2}{y_Q (x_P + z_P) - y_P (z_Q + x_Q)} : \frac {c^2}{z_Q (x_P + y_P) - z_P (x_Q + y_Q)} \right).$ Denote $K'$ is the isogonal conjugate of a point $K$ with respect to $\triangle ABC.$ $K' = \left( x_Q (y_P + z_P) - x_P (y_Q + z_Q) : y_Q (x_P + z_P) – y_P (z_Q + x_Q) : z_Q (x_P + y_P) – z_P (x_Q + y_Q) \right).$ $x_{K'} + y_{K'} + z_{K'} = 0 \implies K \in \Omega.$ If we use NBC, we get $K = \left( \frac {a^2}{x_Q - x_P} : \frac {b^2}{y_Q - y_P } : \frac {c^2}{z_Q - z_P } \right) \implies K' = (x_Q - x_P : y_Q - y_P : z_Q - z_P).$ $L = EP \cap FQ = \left( \frac {1}{\frac {b^2} {x_Q y_P} - \frac {b^2} {x_P y_Q}+ \frac {c^2} {x_Q z_P}- \frac {c^2} {x_Q z_P}} : \frac {1}{\frac {a^2} {x_Q y_P} - \frac {a^2} {x_P y_Q}+ \frac {c^2} {z_Q y_P}- \frac {c^2} {y_Q z_P}} : \frac {1}{\frac {a^2} {x_Q z_P} - \frac {a^2} {x_P z_Q}+ \frac {b^2} {y_Q z_P}- \frac {b^2} {y_P z_Q}} \right).$ $x_{L'} + y_{L'} + z_{L'} = 0 \implies L \in \Omega.$ If we use NBC, we get $L = \left( \frac {a^2}{x_{Q'} - x_{P'}} : \frac {b^2}{y_{Q'} - y_{P'} } : \frac {c^2}{z_{Q'} - z_{P'} } \right) \implies L' = (x_{Q'} - x_{P'} : y_{Q'} - y_{P'} : z_{Q'} - z_{P'}).\blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

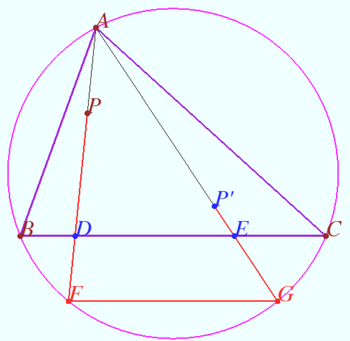
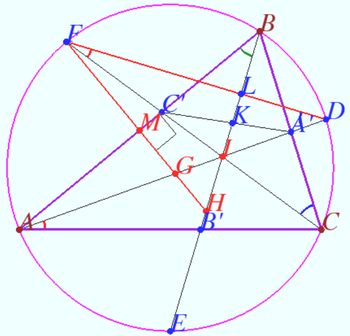
Collinearity for two pares of isogonal points

Let triangle $\triangle ABC,$ and points $P$ and $Q$ be given. Let point $P'$ and $Q'$ be the isogonal conjugate of the points $P$ and $Q$ with respect to a triangle $\triangle ABC, \Omega = \odot ABC.$

Denote $R = PQ \cap P'Q', \theta = \odot P'QR, F = \Omega \cap \theta \notin \odot PQ'R, D \in \Omega$ is the point isogonal conjugate to line $PQ$ with respect $\triangle ABC.$ Isogonal_bijection_lines_and_points

Prove that points $D, P',$ and $F$ are collinear.

Proof

$P = (x_P : y_P : z_P), Q = (x_Q : y_Q : z_Q), P' = \left (\frac {a^2}{x_P} : \frac {b^2}{y_P} : \frac {c^2}{z_P} \right ).$ After the simple calculations one can get:

$PQ: (y_P z_Q - z_P y_Q) x + (x_Q z_P - x_P z_Q) y + (x_P y_Q - x_Q y_P)z = 0.$ $R = \left (\frac {a^2(c^2 y_P y_Q - b^2 z_P z_Q)}{y_Q z_P - z_Q y_P} : \frac {b^2(a^2 z_P z_Q - c^2 x_P x_Q)}{z_Q x_P - x_Q z_P} : \frac {c^2(b^2 x_P x_Q - a^2 y_P y_Q)}{x_Q y_P - y_Q x_P} \right ),$ $F = \left (\frac {a^2}{x_P (y_Q z_P - z_Q y_P)} : \frac {b^2}{y_P (z_Q x_P - x_Q z_P)} : \frac {c^2}{z_P (x_Q y_P - y_Q x_P)} \right ).$ We use the normalized barycentric coordinates NBC and get line $PQ$ in the form of: $PQ = (x_P - x_Q : y_P - y_Q : z_P - z_Q).$ $(x_P - x_Q) + (y_P - y_Q) + (z_P - z_Q) = (x_P + y_P + z_P) - (x_Q + y_Q + z_Q) = 1 - 1 = 0 \implies$ $D = \left (\frac {a^2}{x_P - x_Q} : \frac {b^2}{y_P - y_Q} : \frac {c^2}{z_P - z_Q} \right ).$ We check the condition of collinearity for points $D, F,$ and $P'$ and finishing the proof. $\blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Points on bisectors

Let a triangle $\triangle ABC, BC = a, AC = b, AB = c$ be given.

Let segments $AA', BB',$ and $CC'$ be the bisectors of $\triangle ABC.$

The lines $AA', BB',$ and $CC'$ meet circumcircle $ABC (\Omega$ ) at points $D, E, F,$ respectively. $M$ is the midpoint $AB.$ Denote $G = FM \cap AD, H = FM \cap BE, K = BE \cap A'C', L = BE \cap FD.$

We will find barycentric coordinates of the points and length of the segments. $A= (1:0:0), B= (0:1:0), C= (0:0:1), I=(a:b:c),$ $A'= (0:b:c), B'= (a:0:c), C'= (a:b:0), M = (1:1:0).$ Line $AA'$ is $cy=bz,$ line $BB'$ is $cx=az,$ line $CC'$ is $bx=ay.$

Circle $\Omega$ is $xyc^2 + xzb^2 + yza^2 = 0.$ $D = \Omega \cap AA', D= \left( - \frac {a^2}{b+c}:b:c \right), E = \Omega \cap BB', E = \left(a: - \frac {b^2}{a+c}:c \right),$ $F = \Omega \cap CC', F = \left(a:b: - \frac {c^2}{a+b} \right), K = BE \cap A'C', K = (a : 2b : c)$

Line $DF$ is $x \frac {b+c}{a} +y + z\frac {a+b}{c} = 0.$

Point $L = BE \cap DF, L = (a : a+2b+c : c).$

Line $FM$ is $x = y + z \frac {b^2 - a^2}{c^2}.$

Point $G = AD \cap FM, G = \left( b+ \frac {b^2-a^2}{c} :b: c \right).$

Point $H = BE \cap FM, H = \left( a: a - \frac {b^2-a^2}{c} : c \right).$

Some simple formulas: $\frac {FM}{GM} = \frac {b+c-a}{a+b-c}; \frac {FM}{FG} = \frac {b+c-a}{2b};$ $\frac {FM}{FH} = \frac {a+c-b}{2a}; \frac {GM}{FG} = \frac {a+b-c}{2b};$ $\frac {EH}{B'E} = \frac {a(a+c)}{b^2}; \frac {IH}{B'E} = \frac {|a-b|(a+c)}{b^2};$ $\frac {B'I}{IE} = 1 - \frac {b}{a+c}; \frac {IB}{2} = IL = BL.$ Circumcenter $O \in FM , O = \left( a^2(b^2+c^2 -a^2) : b^2(a^2 + c^2 – b^2) : c^2(a^2 + b^2 - c^2) \right).$

Tangent $BN$ is $c^2 x + a^2 z = 0.$

Line $NI || AC$ is $\left( \frac {b}{a+c} = \frac{y}{x+z} \right).$ $N = BN \cap IN, N = (a^2 : b(a - c) : -c^2).$ $BN = IN = \frac {abc}{|a-c|(a+b+c)}.$ $\frac{HO}{BO} = \frac {|a-c|}{b}; \frac{GO}{BO} = \frac {|b-c|}{a}.$ $Q$ is the midpoint $BB', QP \perp BB', P \in AD \implies P = \left( \frac {a(b-a)}{c} : b : c\right).$ $G = FM \cap AD = \left( \frac {b^2-a^2}{c} : b : c\right).$ $\frac {PD}{GP} = \frac {a}{c}; \frac {FM}{GM} = \frac {b+c-a}{a+b-c};$ $\frac {IC'}{FC'} = \frac {a+b-c}{c}; \frac {IA'}{DA'} = \frac {b+c-a}{a};$ $\frac {ND}{NF} = \frac {a(a+b-c)}{c(b+c-a)}.$

vladimir.shelomovskii@gmail.com, vvsss

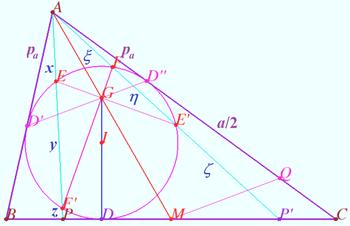
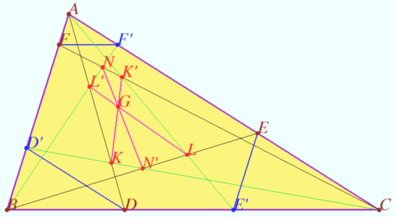
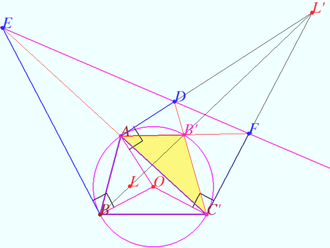
Crosspoint of median and set of secants

Triangle $ABC$ and point $P \in BC$ be given. The incircle $\omega$ of $\triangle ABC$ touches side $BC$ at point $D.$ Point $P'$ is symmetrical to point $P$ with respect midpoint $M$ of $BC.$ The common points of segments $AP$ and $AP'$ with $\omega$ form a convex quadrilateral $EFE'F'.$

Prove that point $G = DI \cap AM$ lies on $EF.$

Proof

Denote $p_a = \frac{b+c-a}{2}, p_b = \frac{a-b+c}{2}, p_c = \frac{a+b-c}{2}, m = \sqrt{\frac {CP}{BP}}.$ $D = \left (0 : p_c : p_b \right), P= \left (0: m: \frac{1}{m}\right), P' = \left ( 0: \frac{1}{m}: m\right).$ $\omega:\hspace{10mm} {p_a}^2x^2 + p_b^2y^2 + p_c^2z^2 - 2p_a p_b xy - 2p_a p_c xz - 2p_bp_cyz = 0,$ Line $AP: \frac {y}{m} = z \cdot m,$ line $AP' : y \cdot m = \frac {z}{m}.$

We solve the system of these equations and get: $E = \left( \left(\sqrt{\frac {p_c}{m}} + \sqrt {p_b \cdot m} \right)^2 : mp_a : \frac {p_a}{m} \right),$ $F' = \left( \left(\sqrt{\frac {p_c}{m}} - \sqrt {p_b \cdot m} \right)^2 : mp_a : \frac {p_a}{m} \right),$ $F = \left( \left(\sqrt{p_c \cdot m} + \sqrt {\frac {p_b}{m}} \right)^2 : \frac {p_a}{m} : mp_a \right),$ $E' = \left( \left(\sqrt{p_c \cdot m} - \sqrt {\frac {p_b}{m}} \right)^2 : \frac {p_a}{m} : mp_a \right).$ We find the lines $EE'$ and $FF',$ we solve the system of equations for this lines and get: $G = \left (a: pa : pa \right ).$ This point lies at the line $AM, \frac {AG}{GM} =\frac {2 p_a}{a}.$ Point $G$ lies at line $DI$ and $\frac {DI}{GI} = \frac {b+c}{a}.$

Corollary

Denote $D' = AB \cap \omega, D'' = AC \cap \omega.$ Then $\frac {D'G}{D''G} = \frac {b}{c}.$

vladimir.shelomovskii@gmail.com, vvsss

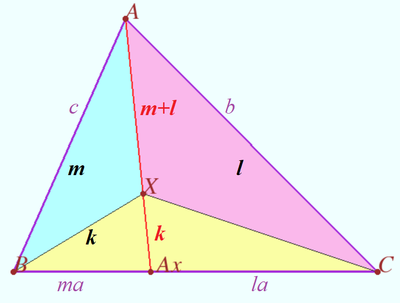
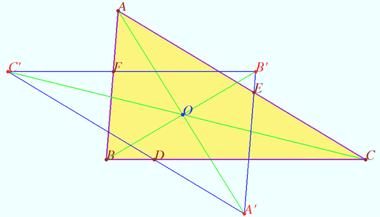
Set of lines in triangle

Let triangle $\triangle ABC$ and points $D$ at the line $BC, E \in AC, F \in AB$ be given.

Denote $D'$ point in $AB$ such that $DD'||AC.$ Similarly, $E' \in BC, EE'||AB, F' \in AC, FF'||BC.$

$K = AD \cap CD', K' = CE \cap AE', L = BE \cap AE',$ $L' = AD \cap BF', N = CF \cap BF', N' = BE \cap CD'.$

Prove that lines $KK', LL',$ and $NN'$ are concurrent.

Proof

Let $d = \frac {CD}{BD}, e = \frac{BF}{AF}, f = \frac{BF}{AF}.$

Then $D = (0: d: 1), E = (1: 0: e), F = (f: 1: 0).$ $DD' || AC \implies D' = (1 :d : 0), EE' || AB \implies E' = (0 :1 : e), FF' || BC \implies F' = (f : 0 : 1).$ $K = (1 : d : 1), L = (1 : 1 : e), N = (f : 1 : 1), K' = (f : 1 : e), L' = (f : d : 1), N' = (1 : d : e).$

Point $G = (1 +f : 1 + d : 1 + e)$ lies at lines $KK', LL',$ and $NN'.$

vladimir.shelomovskii@gmail.com, vvsss

Set of parallel lines

Let triangle $\triangle ABC$ and points $D$ at the line $BC, E \in AC, F \in AB$ be given.

Denote $d = \frac {CD}{BD}, e = \frac{BF}{AF}, f = \frac{BF}{AF}.$

Let $A'$ be the point such that $A'E||AB, A'D||AC.$

Similarly, $B'E||AB, B'F||BC, C'D||AC, C'F||BC.$

Prove that lines $AA', BB',$ and $CC'$ are concurrent.

Find the condition that $\triangle ABC = \triangle A'B'C'.$

Proof

One can get $A' = \left ( \frac {1}{d \cdot e}-1 : 1 + \frac {1}{e} : 1 + \frac {1}{d} \right ),$ $B' = \left (1 + \frac {1}{e} : \frac {1}{e \cdot f}-1 : 1 + \frac {1}{f} \right ), C' = \left (1 + \frac {1}{d} : 1 + \frac {1}{f} : \frac {1}{d \cdot f}-1 \right ),$ $O = \left (\frac {f}{1+f} : \frac {d}{1+d} : \frac {e}{1 + e} \right ), \frac {A'O}{AO} = \frac{B'O}{BO} = \frac {C'O}{CO} = \frac{2def + df + de + ef - 1}{(1+d)(1+ e)(1+f)}.$ If $\frac {A'O}{AO} = 1$ then $def = d+e+f+1.$

Corollary

Let points $D, E,$ and $F$ lie at the lines $BC, AC,$ and $AB.$

Denote circle $\omega = \odot DEF,$ $D' = \omega \cap BC, E' = \omega \cap AC, F' = \omega \cap AB.$

Let $ED' || DE', D'F' || E'F, DF' || FE,$ $A' = DF' \cap D'E, B' = D'E \cap E'F, C' = DF' \cap E'F.$

Then lines $AA', BB',$ and $CC'$ are concurrent.

WLOG, situation is shown on diagram.

The proof contain calculations started from $\triangle A'B'C'$ and finished at $\triangle ABC.$

vladimir.shelomovskii@gmail.com, vvsss

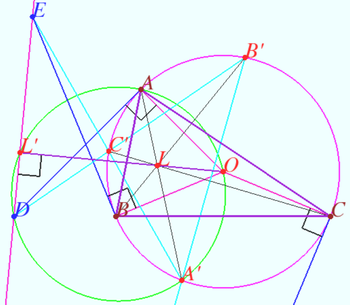
Feuerbach point of a scalene triangle

The Feuerbach point of a scalene triangle lies on one of its bisectors. Prove that the angle corresponding to this bisector is $60^\circ.$

Proof

Denote $ABC -$ given triangle, $a = BC,b = AC,c = AB, I -$ the incenter, $F \in BI$ - the Feuerbach point.

The barycentric coordinates of point $F = \left ((b+c-a)(b-c)^2 : (a+c-b)(a-c)^2 : (a+b-c)(a-b)^2 \right ).$

$F \in BI \implies a \cdot (a+b-c)(a-b)^2 = c \cdot (b+c-a)(b-c)^2 \implies$ $(a - c) \cdot (a + c - b) \cdot (a^2- b^2 - ac + c^2) = 0 \implies$ $b^2 = c^2 + a^2 - ac \implies \angle ABC = 60^\circ.$ Another proof Scalene triangle with angle 60^\circ .

vladimir.shelomovskii@gmail.com, vvsss

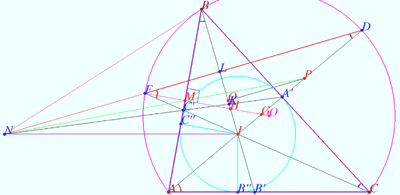
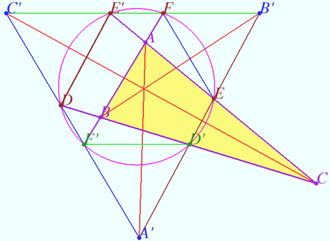
Small Pascal's theorem

Let $\triangle ABC$ and point $P$ be given. Let $\Omega$ be the circumcircle of $\triangle ABC,$ $A' = AP \cap \Omega, B' = BP \cap \Omega, C' = CP \cap \Omega.$ Let the tangent line to $\Omega$ at point $A$ cross line $B'C'$ at point $D.$ Similarly denote points $E$ and $F.$

Prove that the points $D, E$ and $F$ are collinear.

Proof

1. Simplest case, $P$ is the Lemoine point, $P = L = (a^2 : b^2 : c^2).$

The equation of $\Omega$ is $xyc^2 + xzb^2 + yza^2 = 0.$

Line $AP$ is $k = 0, l y_P + m z_P = 0 \implies y c^2 - z b^2 = 0 \implies$ $A' = \left(-\frac{a^2}{2} : b^2 : c^2 \right), B' = \left(a^2 : -\frac{b^2}{2} : c^2 \right), C' = \left(a^2 : b^2 : -\frac{c^2}{2} \right).$ The line $B'C'$ is $\frac{x}{2a^2} - \frac{y}{b^2} - \frac{z}{c^2} = 0 \implies D = \left( 0 : b^2 : - c^2 \right).$

Similarly, $E = ( a^2 : 0 : - c^2), F = (a^2 : - b^2 : 0).$

The line $DEF$ is $\frac {x}{a^2} + \frac {y}{b^2} + \frac {z}{c^2} = 0.$

2. Simple case, $P$ is one of the external Lemoine point, $P = L' = (a^2 : - b^2 : c^2).$

This point is the crosspoint of the tangent lines to $\Omega$ in points $A$ and $C,$ so $A' = A, C' = C, B' = \left (a^2 : -\frac{b^2}{2} : c^2 \right ).$ The line $B'C'$ is $b^2 x + 2y a^2 = 0 \implies D = \left( 2a^2 : -b^2 : c^2 \right).$

Similarly, $E = ( a^2 : 0 : - c^2), F = (a^2 : - b^2 : 2c^2).$

The line $DEF$ is $\frac {x}{a^2} + \frac {3y}{b^2} + \frac {z}{c^2} = 0.$

Similarly, if $P = (-a^2 : b^2 : c^2),$ then the line $DEF$ is $\frac {3x}{a^2} + \frac {y}{b^2} + \frac {z}{c^2} = 0.$

If $P = (a^2 : b^2 : -c^2),$ then the line $DEF$ is $\frac {x}{a^2} + \frac {y}{b^2} + \frac {3z}{c^2} = 0.$

These three lines intersect in pairs at points $D, E,$ and $F$ of the line of case 1.

3. Common case. Denote the coordinates of the point $P = (x_P : y_P : z_P).$ The equation of $\Omega$ is $xyc^2 + xzb^2 + yza^2 = 0.$

Line $AP$ is $l z_P + m y_P = 0 \implies A' = \left( \frac{-y_P \cdot z_P a^2}{y_P c^2 + z_P b^2} : y_P :z_P \right ).$

Similarly, $B' = \left (x_P : \frac{-x_P \cdot z_P b^2}{x_P c^2 + z_P a^2} : z_P \right ), C' = \left (x_P : y_P : \frac{-x_P \cdot y_P c^2}{x_P b^2 + y_P a^2} \right ).$

The tangent line $l_A$ to $\Omega$ at $A$ is $yC^2 +zb^2=0.$

The line $B'C'$ is $\frac{y_P \cdot z_P a^2}{x_P} x - (x_P \cdot c^2 + z_P a^2)y - (x_P b^2 +y_Pa^2)z = 0.$

$D = l_A \cap B'C' = \left( x_P (y_P c^2 - z_P b^2) : -y_P \cdot z_P b^2 : y_P \cdot z_P c^2 \right).$

Similarly, $E = l_B \cap A'C' = \left( x_P z_P a^2 : -y_P (x_P c^2 - z_P a^2) : -x_P \cdot z_P c^2 \right).$ $F = l_C \cap A'B' = \left( x_P y_P a^2 : -x_P y_P b^2 : z_P (y_P a^2 - x_P b^2) \right).$ The line $DEF$ is $\frac {x}{x_P} (-\frac {a^2}{x_P} + \frac {b^2}{y_P} + \frac {c^2}{z_P}) + \frac {y}{y_P} (\frac {a^2}{x_P} - \frac {b^2}{y_P} + \frac {c^2}{z_P}) +\frac {z}{z_P} (\frac {a^2}{x_P} + \frac {b^2}{y_P} - \frac {c^2}{z_P}) = 0.$

vladimir.shelomovskii@gmail.com, vvsss

Page

Toolbox

Search

Barycentric coordinates

Contents

Useful formulas

Product of isogonal segments

Ratio of isogonal segments

Point on incircle

Crossing point

Fixed point on circumcircle

Two pare isogonal points

Collinearity for two pares of isogonal points

Points on bisectors

Crosspoint of median and set of secants

Set of lines in triangle

Set of parallel lines

Feuerbach point of a scalene triangle

Small Pascal's theorem