Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2024 AMC 12A Problems/Problem 13

Revision as of 09:30, 24 November 2024 by Oinava (talk | contribs) (→‎Solution 3 (Derivatives))

Problem

The graph of $y=e^{x+1}+e^{-x}-2$ has an axis of symmetry. What is the reflection of the point $(-1,\tfrac{1}{2})$ over this axis?

$\textbf{(A) }\left(-1,-\frac{3}{2}\right)\qquad\textbf{(B) }(-1,0)\qquad\textbf{(C) }\left(-1,\frac{1}{2}\right)\qquad\textbf{(D) }\left(0,\frac{1}{2}\right)\qquad\textbf{(E) }\left(3,\frac{1}{2}\right)$

Solution 1

The line of symmetry is probably of the form $x=a$ for some constant $a$. A vertical line of symmetry at $x=a$ for a function $f$ exists if and only if $f(a-b)=f(a+b)$; we substitute $a-b$ and $a+b$ into our given function and see that we must have

\[e^{a-b+1}+e^{-(a-b)}-2=e^{a+b+1}+e^{-(a+b)}-2\]

for all real $b$. Simplifying:

\begin{align*} e^{a-b+1}+e^{-(a-b)}-2&=e^{a+b+1}+e^{-(a+b)}-2 \\ e^{a-b+1}+e^{b-a}&=e^{a+b+1}+e^{-a-b} \\ e^{a-b+1}-e^{-a-b}&=e^{a+b+1}-e^{b-a} \\ e^{-b}\left(e^{a+1}-e^{-a}\right)&=e^b\left(e^{a+1}-e^{-a}\right). \\ \end{align*}

If $e^{a+1}-e^{-a}\neq0$, then $e^{-b}=e^b$ for all real $b$; this is clearly impossible, so let $e^{a+1}-e^{-a}=0\implies a+1=-a\implies a=-\dfrac12$. Thus, our line of symmetry is $x=-\dfrac12$, and reflecting $\left(-1,\dfrac12\right)$ over this line gives $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}.$

~Technodoggo

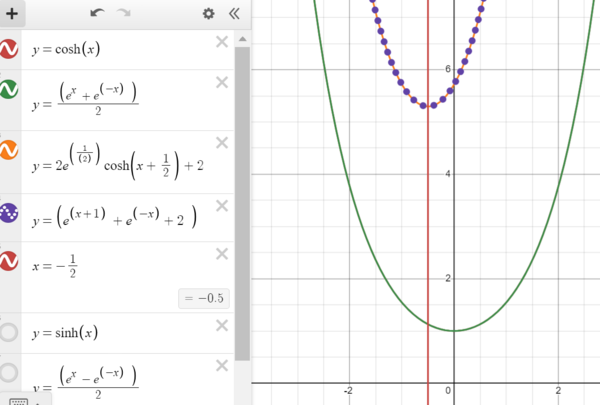
Solution 2 (Graphing cheese)

Consider the graphs of $y=e^{x+1}-1$ and $y=e^{-x}-1$. A rough sketch will show that they intercept somewhere between -1 and 0 and the axis of symmetry is vertical. Thus, $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}$ is the only possible answer.

Note: You can more rigorously think about the solution by noting that since the derivative of the power that e is raised to in one equation is equal to the derivative of the power that e is raised to multiplied by $-1$ and both equations are subtracted by 1, then the sum of both equations will be the same from one side of the interception to the other. Setting both equations equal to each other, it is trivial to see $x=-1/2$, giving us the axis of symmetry.

~woeIsMe

[asy] unitsize(2cm); real e = 2.71828; real f1(real x) {return e^(x+1)-1;} real f2(real x) {return e^(0-x)-1;} draw(graph(f1,-1.5,0.5)); draw(graph(f2,-1.5,0.5)); xaxis(-2,1,Ticks()); yaxis(f2(0.5),f1(0.5),Ticks()); draw((-0.5,f2(0.5))--(-0.5,f1(0.5)),red+dashed); /*graph by Technodoggo, 9 November 2024*/ [/asy] (graph by Technodoggo)

Solution 3 (Derivatives)

Since y is a proper function of x, the axis of symmetry is vertical. Where a function crosses a vertical axis of symmetry, it must have a vertical asymptote (clearly impossible for this given function, since linear functions and exponential function are total functions), or a local maximum or minimum (derivative 0).

So the derivative is equal to 0: $\frac{d[e^{x+1}+e^{-x}-2]}{dx} = 0 = e^{x+1}-e^{-x}$

To solve for $x$, make a substitution: $u = e^x$ $0 = e*u - \frac{1}{u}$ -> $0 = \frac{e*u^2 - 1}{u}$ -> $0 = e*u^2 - 1$ -> $e*u^2 = 1$ -> $(e^x)^2 = \frac{1}{e}$ -> $e^{2x} = e^{-1}$ -> $2x = -1$ -> $x = -\frac{1}{2}$ Now we just flippidy flap (-1, $\frac{1}{2}$) over $x = -\frac{1}{2}$ and blammo, we got ourselves the answer choice $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}.$

Solution 4

\[f(0) = e-1\] \[f(1) = e^2 + e^{-1} - 2\] \[f(-1) = 1+ e -2 = e-1\] \[f(-2) = e^{-1} + e^2 -2\]


so f(0) = f(-1) , f(1) =f(-2) then f(x) is symmetric about x=-1/2 point (-1, 1/2) reflects over axis x=-1/2 is point ( 0, 1/2) answer choice D ~luckuso

Solution 5

Notice that this is simply a transformation of $\cosh(x)$, specifically $2e^\frac{1}{2}\cosh(x + \frac{1}{2}) + 2$. We know that $\cosh(x)$ has a parabolic shape with an axis of symmetry $x=0$. Since this is simple a transformation of $\frac{1}{2}$ to the left of the origin, we have the axis of symmetry is $x = -\frac{1}{2}$ giving us $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}$

~KEVIN_LIU

Solution 5 (Graph)

2024 amc12A p13.PNG

~luckuso

Solution 6

\[f(-x-1) = e^{-x-1+1} + e^{-(-x-1)} - 2 = e^{-x} + e^{x+1} - 2 = f(x)\]

So the axis is $\frac{x + (-x + 1)}{2} = -1/2$

Point $(-1, 1/2)$ reflects over the axis $x=-1/2$ to the point $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}$

~luckuso

Solution 7

Setting the axis of symmetry as $x=a$ implies $f(2a-x) = f(x)$

\begin{align*} f(2a-x) &= f(x) \\ e^{2a-x+1} + e^{-(2a-x)} - 2 &= e^{x+1} + e^{-x} - 2 \end{align*}

Analyzing the terms $e^{2a-x+1}$ and $e^{-x}$ tells us that $2a+1 = 0$

This reveals that $a = -1/2$


Finally, point $(-1, 1/2)$ reflected over the axis $x=-1/2$ is the point $\boxed{\textbf{(D) }\left(0,\dfrac12\right)}$

~luckuso

See also

2024 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 12 		Followed by
Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_AMC_12A_Problems/Problem_13&oldid=235462"