2024 AMC 10A Problems/Problem 24

Problem

A bee is moving in three-dimensional space. A fair six-sided die with faces labeled $A^+, A^-, B^+, B^-, C^+,$ and $C^-$ is rolled. Suppose the bee occupies the point $(a,b,c).$ If the die shows $A^+$ , then the bee moves to the point $(a+1,b,c)$ and if the die shows $A^-,$ then the bee moves to the point $(a-1,b,c).$ Analogous moves are made with the other four outcomes. Suppose the bee starts at the point $(0,0,0)$ and the die is rolled four times. What is the probability that the bee traverses four distinct edges of some unit cube?

$\textbf{(A) }\frac{1}{54}\qquad\textbf{(B) }\frac{7}{54}\qquad\textbf{(C) }\frac{1}{6}\qquad\textbf{(D) }\frac{5}{18}\qquad\textbf{(E) }\frac{2}{5}$

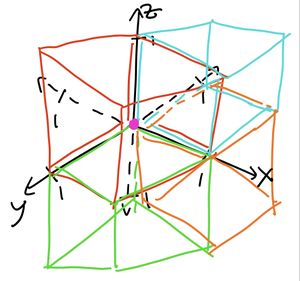
Diagram by PaperMath

~ Diagram by PaperMath

Solution 1

Without loss of generality, assume that the first two moves are equal for all possible combinations, since the direction does not matter. The first move has a $\frac{6}{6}$ probability of being along one of the $8$ unit cubes around the origin, and the second move has a $\frac{4}{6}$ chance. Now, there are two cases. We are currently on one of the points of the $2$ by $2$ squares that are aligned with the axes. The first case is if the bee moves to the corner of a cube farthest away from the origin. Here, there is a $\frac{2}{6}$ chance of this happening and a $\frac{2}{6}$ chance of the fourth move remaining on one of the cubes. The second case is if the bee moves along the same plane of the $2$ by $2$ squares previously, ending up on a point 1 away from the origin. There is a $\frac{1}{6}$ chance of this happening and a $\frac{3}{6}$ chance of remaining on one of the cubes. Now, multiply and sum for the answer. $\frac{2}{3}\cdot(\frac{1}{3}\cdot\frac{1}{3}+\frac{1}{6}\cdot\frac{1}{2})=\frac{2}{3}\cdot(\frac{1}{9}+\frac{1}{12})$ Evaluating this gives you the answer of $\boxed{\textbf{(B) }\frac{7}{54}}$ . Solution by juwushu. Minor edits by andliu766

Solution 2

Remove the dice. It is not necessary for this problem. It is the same problem if you instead view this problem as the bee moving one up or down in the $x, y,$ and $z$ directions.

Count the total number of ways for one cube of the 8 total ones. It is not hard to see that after the first step (which you can travel to $(1,0,0), (0,1,0),$ or $(0,0,1)$ - 3 ways), you have a total of 8 moves to traverse a face of that 1x1 cube. Hence, for each cube, you would have $8 \cdot 3 = 24$ total moves.

There are a total of 8 cubes you could have traversed, though, so multiplying this by $8$ yields $8 \cdot 8 \cdot 3.$

We have to account for overcounting. For example, when we traversed the face in the $xz$ plane $(0,0,0), (0,0,1),(1,0,0),(1,0,1),$ the number of ways that we traverse that particular face got counted twice, once from the cube in the far upper right and once from the cube in the closer upper right.

For a given face, you can go clockwise or counterclockwise, hence yielding $2$ ways. There are a total of $12$ shared faces, each one shared by exactly two faces so no additonal PIE is needed. We simply subtract $2\cdot12$ from our original count now, yielding $8 \cdot 3 \cdot 8 - 2 \cdot 12 = 168.$

With no restrictions, there are a total of $6^4$ ways to move four steps. Your probability is $\frac{168}{6^4}=\frac{7}{54}.$

~mathboy282

Video Solution by Innovative Minds

https://youtu.be/CxLGUPhYYDI

~i_am_suk_at_math_2

2024 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 23	Followed by Problem 25
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search