DVI exam
Contents
2020 201 problem 6
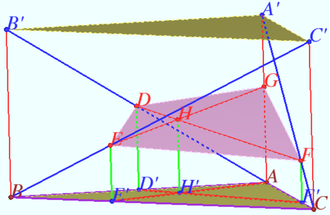
Let a triangular prism ![]() with a base
with a base ![]() be given,
be given, ![]() Find the ratio in which the plane
Find the ratio in which the plane ![]() divides the segment
divides the segment ![]() if
if ![]()
![]()
Solution
Let ![]() be the parallel projections of
be the parallel projections of ![]() on the plane
on the plane ![]()
![]()
We use and get
![]()
![]() Let
Let ![]()
Similarly ![]()
Answer: ![]()
2020 202 problem 6
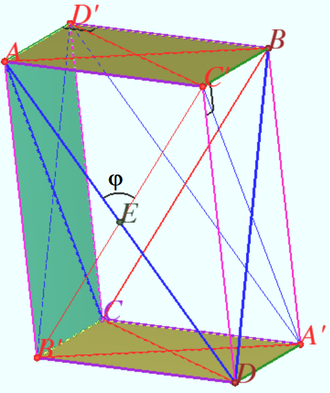
Let a tetrahedron ![]() be given,
be given, ![]() Find the cosine of the angle
Find the cosine of the angle ![]() between the edges
between the edges ![]() and
and ![]()
Solution
Let us describe a parallelepiped ![]() around a given tetrahedron
around a given tetrahedron ![]()
![]() and
and ![]() are equal rectangles.
are equal rectangles.
![]() and
and ![]() are equal rectangles.
are equal rectangles.
Denote ![]()
![]()
![]()
![]()
![]() Answer:
Answer: ![]()
2020 203 problem 6
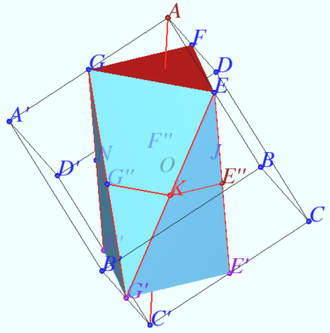
Let a cube ![]() with the base
with the base ![]() and side edges
and side edges ![]() be given. Find the volume of a polyhedron whose vertices are the midpoints of the edges
be given. Find the volume of a polyhedron whose vertices are the midpoints of the edges ![]()
Solution
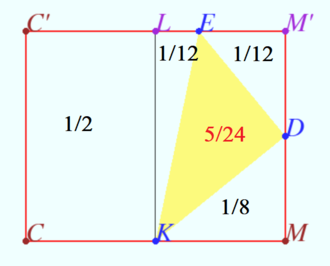
Denote the vertices of polyhedron ![]() Triangles
Triangles ![]() and
and ![]() are equilateral triangles with sides
are equilateral triangles with sides ![]() and areas
and areas ![]()
This triangles lies in parallel planes, which are normal to cube diagonal ![]() The distance
The distance ![]() between this planes is
between this planes is ![]() So the volume of the regular prism with base
So the volume of the regular prism with base ![]() and height
and height ![]() is
is
![]()
Let the area ![]() be the quadratic function of
be the quadratic function of ![]() Let
Let
![]()
![]() Suppose, we move point
Suppose, we move point ![]() along axis
along axis ![]() and cross the solid by plane contains
and cross the solid by plane contains ![]() and normal to axis. Distance from
and normal to axis. Distance from ![]() to each crosspoint this plane with the edge change proportionally position
to each crosspoint this plane with the edge change proportionally position ![]() along axes, so the area is quadratic function from position.
along axes, so the area is quadratic function from position.
![]()
![]()
Answer: ![]()
2022 221 problem 7
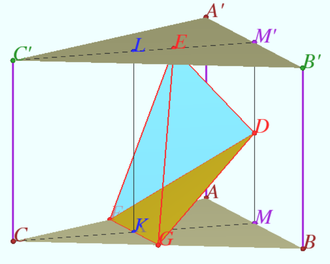
The volume of a triangular prism ![]() with base
with base ![]() and side edges
and side edges ![]() is equal to
is equal to ![]() Find the volume of the tetrahedron
Find the volume of the tetrahedron ![]() where
where ![]() is the centroid of the face
is the centroid of the face ![]() is the point of intersection of the medians of
is the point of intersection of the medians of ![]() is the midpoint of the edge
is the midpoint of the edge ![]() and
and ![]() is the midpoint of the edge
is the midpoint of the edge ![]()
Solution
Let us consider the uniform triangular prism ![]() Let
Let ![]() be the midpoint of
be the midpoint of ![]() be the midpoint of
be the midpoint of ![]() be the midpoint of
be the midpoint of ![]() be the midpoint of
be the midpoint of ![]()
The area ![]() of
of ![]() in the sum with the areas of triangles
in the sum with the areas of triangles ![]() is half the area of rectangle
is half the area of rectangle ![]() so
so
![]()
![]() Denote the distance between these lines
Denote the distance between these lines ![]() The volume of the tetrahedron is
The volume of the tetrahedron is ![]()
![]() The volume of the prism is
The volume of the prism is ![]()
![]()
An arbitrary prism is obtained from a regular one as a result of an affine transformation.
All points on the tetrahedron are defined affinely, which means that the volume ratio will be preserved.
Answer: 5.
2022 222 problem 7
A sphere of diameter ![]() is inscribed in a pyramid at the base of which lies a rhombus with an acute angle
is inscribed in a pyramid at the base of which lies a rhombus with an acute angle ![]() and side
and side ![]() Find the angle
Find the angle ![]() if it is known that all lateral faces of the pyramid are inclined to plane of its base at an angle of
if it is known that all lateral faces of the pyramid are inclined to plane of its base at an angle of ![]()
Solution 1
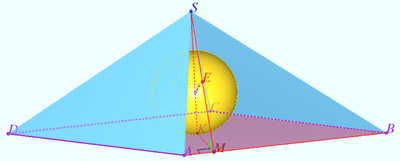
Denote rhombus ![]() is the vertex of a pyramid
is the vertex of a pyramid ![]() is the center of the sphere,
is the center of the sphere, ![]() is the tangent point of
is the tangent point of ![]() and sphere,
and sphere, ![]()
![]()
![]()
![]()
![]() Solution 2
Solution 2
The area of the rhombus ![]()
The area of the lateral surface is ![]()
![]()
![]() Answer:
Answer:![]()