1997 AIME Problems/Problem 6
Problem
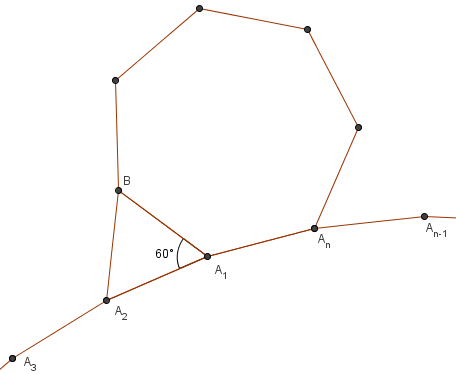
Point ![]() is in the exterior of the regular
is in the exterior of the regular ![]() -sided polygon
-sided polygon ![]() , and
, and ![]() is an equilateral triangle. What is the largest value of
is an equilateral triangle. What is the largest value of ![]() for which
for which ![]() ,
, ![]() , and
, and ![]() are consecutive vertices of a regular polygon?
are consecutive vertices of a regular polygon?
Solution
Let the other regular polygon have ![]() sides. Using the interior angle of a regular polygon formula, we have
sides. Using the interior angle of a regular polygon formula, we have ![]() ,
, ![]() , and
, and ![]() . Since those three angles add up to
. Since those three angles add up to ![]() ,
,
 Using SFFT,
Using SFFT,
![]() Clearly
Clearly ![]() is maximized when
is maximized when ![]() .
.
See also
| 1997 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||