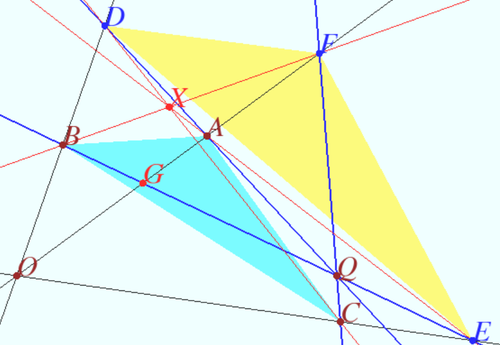
Double perspective triangles

Two triangles in double perspective are in triple perspective

Let $\triangle ABC$ and $\triangle DEF$ be in double perspective, which means that triples of lines $AF, BD, CE$ and $AD, BE, CF$ are concurrent. Prove that lines $AE, BF,$ and $CD$ are concurrent (the triangles are in triple perspective).

Proof

Denote $G = AF \cap BE.$

It is known that there is projective transformation that maps any quadrungle into square.

We use this transformation for $BDFG$ . We use the Claim for square and get the result: lines $AE, BF,$ and $CD$ are concurrent.

Claim for square Let $ADBG$ be the square, let $CEGF$ be the rectangle, $A \in FG, G \in BE.$ Prove that lines $BF, CD,$ and $AE$ are concurrent.

Proof

Let $BG = a, GE = b, AF = c, A = (0,0).$ Then

\[B=(− a, − a), F = (0,c), BF: y= x (1 + \frac {c}{a})+c.\] (Error compiling LaTeX. Unknown error_msg)

\[E=(b, − a),  AE: y = − \frac {a}{b}x.\] (Error compiling LaTeX. Unknown error_msg)

\[D = (−a,0), C= (b,c), CD: y = c \frac {x+a}{a+b}.\] (Error compiling LaTeX. Unknown error_msg)

$X = CD \cap AE \cap BF = (− b, a) \frac {c}{a+b +{\frac {bc}{a}}$ (Error compiling LaTeX. Unknown error_msg) as desired.

vladimir.shelomovskii@gmail.com, vvsss

Page

Toolbox

Search

Double perspective triangles

Two triangles in double perspective are in triple perspective