Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Kimberling’s point X(24)

Revision as of 13:26, 12 October 2022 by Vvsss (talk | contribs) (→‎Theorem 2)

Kimberling's point X(24)

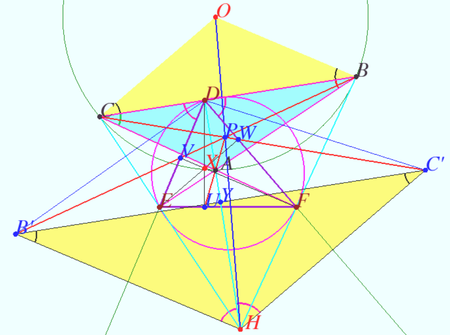
2016 USAMO 3g.png

Kimberling defined point X(24) as perspector of $\triangle ABC$ and Orthic Triangle of the Orthic Triangle of $\triangle ABC$.

Theorem 1

Denote $T_0$ obtuse or acute $\triangle ABC.$ Let $T_0$ be the base triangle, $T_1 = \triangle DEF$ be Orthic triangle of $T_0, T_2 = \triangle UVW$ be Orthic Triangle of $T_1$. Let $O$ and $H$ be the circumcenter and orthocenter of $T_0.$

Then $\triangle T_0$ and $\triangle T_2$ are homothetic, the point $P,$ center of this homothety lies on Euler line $OH$ of $T_0.$

The ratio of the homothety is $k = \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.$

Proof

WLOG, we use case $\angle A = \alpha > 90^\circ.$

Let $B'$ be reflection $H$ in $DE.$ In accordance with Claim, $\angle BVD = \angle HVE \implies B', V,$ and $B$ are collinear.

Similarly, $C, W,$ and $C',$ were $C'$ is reflection $H$ in $DF,$ are collinear.

Denote $\angle ABC = \beta = \angle CHD, \angle ACB = \gamma = \angle BHD \implies$

$\angle HDF = \angle HDE = \angle DHB' = \angle DHC' = 180^\circ - \alpha.$

$B'C' \perp HD, BC \perp HD \implies BC|| B'C'.$ $OB = OC, HB' = HC', \angle BOC = \angle B'HC' = 360^\circ - 2 \alpha \implies OB ||HB', OC || HC' \implies$

$\triangle HB'C' \sim \triangle OBC, BB', CC'$ and $HO$ are concurrent at point $P.$

In accordance with Claim, $\angle HUF = \angle AUF \implies$ points $H$ and $P$ are isogonal conjugate with respect $\triangle UVW.$

\[\angle HDE = \alpha - 90^\circ, \angle HCD = 90^\circ - \beta \implies\]

\[HB' = 2 HD \sin (\alpha - 90^\circ) = - 2 CD \tan(90^\circ- \beta) \cos \alpha = - 2 AC \cos \gamma \frac {\cos \beta}{\sin \beta} \cos \alpha = - 4 OB \cos A \cos B \cos C.\] \[k = \frac {HB'}{OB} = \frac {HP}{OP}= - 4 \cos A \cos B \cos C \implies \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.\]

Claim

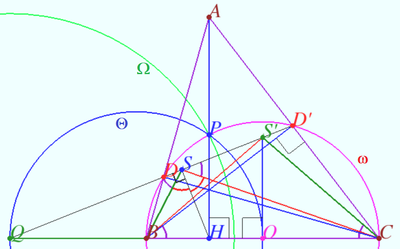
2016 3 Lemma.png

Let $\triangle ABC$ be an acute triangle, and let $AH, BD',$ and $CD$ denote its altitudes. Lines $DD'$ and $BC$ meet at $Q, HS \perp DD'.$ Prove that $\angle BSH = \angle CSH.$

Proof

Let $\omega$ be the circle $BCD'D$ centered at $O (O$ is midpoint $BC).$

Let $\omega$ meet $AH$ at $P.$ Let $\Omega$ be the circle centered at $Q$ with radius $QP.$

Let $\Theta$ be the circle with diameter $OQ.$

Well known that $AH$ is the polar of point $Q,$ so $QO \cdot HO = QP^2 \implies QB \cdot QC = (QO – R) \cdot (QO + R) = QP^2$ \[\implies P \in \Theta, \Omega \perp \omega.\]

Let $I_{\Omega}$ be inversion with respect $\Omega, I_{\Omega}(B) = C, I_{\Omega}(H) = O,I_{\Omega}(D) = D'.$

Denote $I_{\Omega}(S) = S'.$

\[HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.\] \[\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.\] \[\angle BSH = 90 ^\circ – \angle QSB = 90 ^\circ – \angle CSS' =\angle CSH.\]

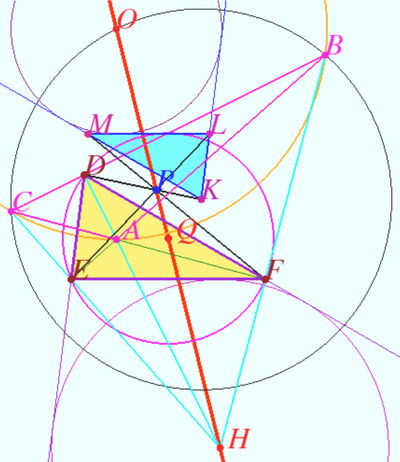
Theorem 2

2016 USAMO 3e.png

Let $T_0 = \triangle ABC$ be the base triangle, $T_1 = \triangle DEF$ be orthic triangle of $T_0, T_2 = \triangle KLM$ be Kosnita triangle of $T_0.$ Then $\triangle T_1$ and $\triangle T_2$ are homothetic, the point $P,$ center of this homothety lies on Euler line of $T_0,$ the ratio of the homothety is $k = \frac {\vec PH}{\vec OP} = 4 \cos A \cos B \cos C.$ We recall that vertex of Kosnita triangle are: $K$ is the circumcenter of $\triangle OBC, L$ is the circumcenter of $\triangle OAB, M$ is the circumcenter of $\triangle OAC,$ where $O$ is circumcenter of $T_0.$

Proof

Let $H$ be orthocenter of $T_0, Q$ be the center of Nine-point circle of $T_0, HQO$ is the Euler line of $T_0.$ Well known that $EF$ is antiparallel $BC$ with respect $\angle A.$

$LM$ is the bisector of $AO,$ therefore $LM$ is antiparallel $BC$ with respect $\angle A$ \[\implies LM||EF.\] Similarly, $DE||KL, DF||KM \implies \triangle DEF$ and $\triangle KLM$ are homothetic.

Let $P$ be the center of homothety.

$H$ is $D$-excenter of $\triangle DEF, O$ is $K$-excenter of $\triangle KLM \implies$ $P \in HO.$

Denote $a = BC, \alpha = \angle A, \beta = \angle B, \gamma = \angle C, R$ circumradius $\triangle ABC.$ $\angle EHF = 180^\circ - \alpha, EF = BC |\cos \alpha| = 2R \sin \alpha |\cos \alpha|.$ $LM = \frac {R}{2} (\tan \beta + \tan \gamma) = \frac {R \sin (\beta + \gamma)}{2 \cos \beta \cdot \cos \gamma} \implies$ \[k = \frac {DE}{KL} = 4\cos \alpha \cdot \cos \beta \cdot \cos \gamma.\] $\frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C \implies P$ is point $X(24).$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Kimberling’s_point_X(24)&oldid=179073"