2019 IMO Problems/Problem 6
Problem
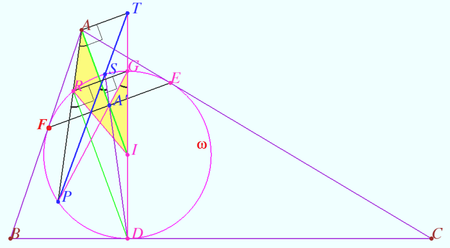
Let ![]() be the incenter of acute triangle
be the incenter of acute triangle ![]() with
with ![]() . The incircle
. The incircle ![]() of
of ![]() is tangent to sides
is tangent to sides ![]() ,
, ![]() , and
, and ![]() at
at ![]() ,
, ![]() , and
, and ![]() , respectively. The line through
, respectively. The line through ![]() perpendicular to
perpendicular to ![]() meets
meets ![]() again at
again at ![]() . Line
. Line ![]() meets ω again at
meets ω again at ![]() . The circumcircles of triangles
. The circumcircles of triangles ![]() and
and ![]() meet again at
meet again at ![]() .
Prove that lines
.
Prove that lines ![]() and
and ![]() meet on the line through
meet on the line through ![]() perpendicular to
perpendicular to ![]() .
.
Solution
Step 1
We find an auxiliary point ![]()
Let ![]() be the antipode of
be the antipode of ![]() on
on ![]() where
where ![]() is radius
is radius ![]()
We define ![]()
![]() is cyclic
is cyclic ![]()
![]()
![]() An inversion with respect
An inversion with respect ![]() swap
swap ![]() and
and ![]() is the midpoint
is the midpoint ![]()
Let ![]() meets
meets ![]() again at
again at ![]() We define
We define ![]()
Opposite sides of any quadrilateral inscribed in the circle ![]() meet on the polar line of the intersection of the diagonals with respect to
meet on the polar line of the intersection of the diagonals with respect to ![]() and
and ![]() meet on the line through
meet on the line through ![]() perpendicular to
perpendicular to ![]() The problem is reduced to proving that
The problem is reduced to proving that ![]()
Step 2
We find a simplified way to define the point ![]()
We define ![]()
![]()
![]() and
and ![]() are bisectrices).
are bisectrices).
We use the Tangent-Chord Theorem and get ![]()
![]()
![]()
![]()
Points ![]() and
and ![]() are concyclic.
are concyclic.
Step 3
We perform inversion around ![]() The straight line
The straight line ![]() maps onto circle
maps onto circle ![]() We denote this circle
We denote this circle ![]() We prove that the midpoint of
We prove that the midpoint of ![]() lies on the circle
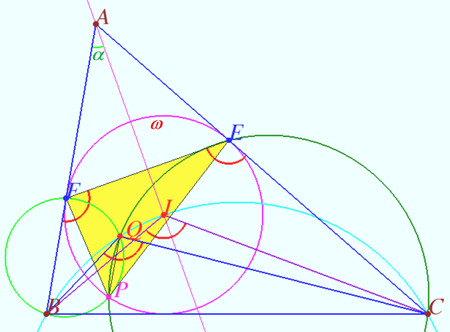
lies on the circle ![]() In the diagram, the configuration under study is transformed using inversion with respect to
In the diagram, the configuration under study is transformed using inversion with respect to ![]() The images of the points are labeled in the same way as the points themselves. Points D,E,F,P,S,G have saved their position. Vertices A, B and C have moved to the midpoints of the segments EF, FD, and DE, respectively.
Let
The images of the points are labeled in the same way as the points themselves. Points D,E,F,P,S,G have saved their position. Vertices A, B and C have moved to the midpoints of the segments EF, FD, and DE, respectively.
Let ![]() be the midpoint
be the midpoint ![]() is parallelogram
is parallelogram ![]() is midpoint
is midpoint ![]() We define
We define ![]()