2020 AIME I Problems/Problem 15

Problem

Let $\triangle ABC$ be an acute triangle with circumcircle $\omega,$ and let $H$ be the intersection of the altitudes of $\triangle ABC.$ Suppose the tangent to the circumcircle of $\triangle HBC$ at $H$ intersects $\omega$ at points $X$ and $Y$ with $HA=3,HX=2,$ and $HY=6.$ The area of $\triangle ABC$ can be written in the form $m\sqrt{n},$ where $m$ and $n$ are positive integers, and $n$ is not divisible by the square of any prime. Find $m+n.$

Solution 1

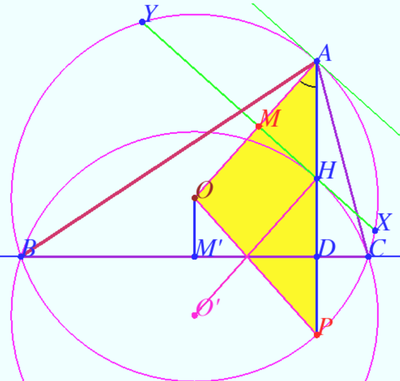
The following is a power of a point solution to this menace of a problem: $[asy] /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki go to User:Azjps/geogebra */ import graph; size(18cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -12.821705655137235, xmax = 10.870448356581754, ymin = -3.0673360097491003, ymax = 10.363346102088961; /* image dimensions */ pen wrwrwr = rgb(0.3803921568627451,0.3803921568627451,0.3803921568627451); /* draw figures */ draw((xmin, 0.0052470390246834855*xmin + 3.437118410441658)--(xmax, 0.0052470390246834855*xmax + 3.437118410441658), linewidth(2) + wrwrwr); /* line */ draw(circle((-4.538171990791266,4.905585481447388), 4.693275552848494), linewidth(2) + wrwrwr); draw(circle((-4.522512329243054,1.9211095752183682), 4.693275552848494), linewidth(2) + wrwrwr); draw((xmin, -190.58367877496823*xmin-1479.5139994609244)--(xmax, -190.58367877496823*xmax-1479.5139994609244), linewidth(2) + wrwrwr); /* line */ draw((xmin, 0.9703333412757664*xmin + 12.849035992754926)--(xmax, 0.9703333412757664*xmax + 12.849035992754926), linewidth(2) + wrwrwr); /* line */ draw(circle((-7.790821079477277,5.289342543424063), 1.8930768158550504), linewidth(2) + wrwrwr); draw((xmin, -1.0305736775830343*xmin-5.438100054565965)--(xmax, -1.0305736775830343*xmax-5.438100054565965), linewidth(2) + wrwrwr); /* line */ draw((xmin, -1.0305736775830343*xmin + 0.22866488339331612)--(xmax, -1.0305736775830343*xmax + 0.22866488339331612), linewidth(2) + wrwrwr); /* line */ /* dots and labels */ dot((-8.98,3.39),dotstyle); label("$B$", (-8.914038694762803,3.548005694821766), NE * labelscalefactor); dot((-0.08068432003432058,3.4366950566657577),dotstyle); label("$C$", (-0.021788682572170717,3.594159241597842), NE * labelscalefactor); dot((-4.538171990791266,4.905585481447388),dotstyle); label("$O$", (-4.483298204259513,5.055688222840243), NE * labelscalefactor); dot((-4.522512329243054,1.9211095752183682),linewidth(4pt) + dotstyle); label("$O'$", (-4.467913688667488,2.0403231668032897), NE * labelscalefactor); dot((-7.790821079477277,5.289342543424063),dotstyle); label("$H$", (-7.729430994176854,5.440301112640874), NE * labelscalefactor); dot((-7.806480741025488,8.273818449653083),linewidth(4pt) + dotstyle); label("$A$", (-7.7448155097688804,8.394128106309726), NE * labelscalefactor); dot((-9.139423209055858,3.980748932978468),linewidth(4pt) + dotstyle); label("$X$", (-9.083268366275083,4.101848256134676), NE * labelscalefactor); dot((-9.752410287411378,3.3859471330788855),linewidth(4pt) + dotstyle); label("$K$", (-9.68326447436407,3.5018521480456903), NE * labelscalefactor); dot((-3.475227037470366,9.476907329794422),linewidth(4pt) + dotstyle); label("$Y$", (-3.4063821128177407,9.594120322487697), NE * labelscalefactor); dot((-7.780888168280388,3.3962917865759925),linewidth(4pt) + dotstyle); label("$L$", (-7.714046478584829,3.5172366636377155), NE * labelscalefactor); dot((-7.776585346090923,2.5762441045932913),linewidth(4pt) + dotstyle); label("$D$", (-7.714046478584829,2.7018573372603765), NE * labelscalefactor); dot((-6.307325123263112,6.728828131386446),linewidth(4pt) + dotstyle); label("$E$", (-6.252517497342424,6.855676547107199), NE * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]$

Let points be what they appear as in the diagram below. Note that $3HX = HY$ is not insignificant; from here, we set $XH = HE = \frac{1}{2} EY = HL = 2$ by PoP and trivial construction. Now, $D$ is the reflection of $A$ over $H$ . Note $AO \perp XY$ , and therefore by Pythagorean theorem we have $AE = XD = \sqrt{5}$ . Consider $HD = 3$ . We have that $\triangle HXD \cong HLK$ , and therefore we are ready to PoP with respect to $(BHC)$ . Setting $BL = x, LC = y$ , we obtain $xy = 10$ by PoP on $(ABC)$ , and furthermore, we have $KH^2 = 9 = (KL - x)(KL + y) = (\sqrt{5} - x)(\sqrt{5} + y)$ . Now, we get $4 = \sqrt{5}(y - x) - xy$ , and from $xy = 10$ we take $\frac{14}{\sqrt{5}} = y - x.$ However, squaring and manipulating with $xy = 10$ yields that $(x + y)^2 = \frac{396}{5}$ and from here, since $AL = 5$ we get the area to be $3\sqrt{55} \implies \boxed{058}$ . ~awang11's sol

Solution 1a

As in the diagram, let ray $AH$ extended hits BC at L and the circumcircle at say $P$ . By power of the point at H, we have $HX \cdot HY = AH \cdot HP$ . The three values we are given tells us that $HP=\frac{2\cdot 6}{3}=4$ . L is the midpoint of $HP$ (see here: https://www.cut-the-knot.org/Curriculum/Geometry/AltitudeAndCircumcircle.shtml ), so $HL=LP=2$ .

As in the diagram provided, let K be the intersection of $BC$ and $XY$ . By power of a point on the circumcircle of triangle $HBC$ , $KH^{2}=KB \cdot KC$ . By power of a point on the circumcircle of triangle $ABC$ , $KB \cdot KC=KX \cdot KY$ , thus $KH^{2}=(KH-2)(KH+6)$ . Solving gives $4KH=12$ or $KH=3$ .

By the Pythagorean Theorem on triangle $HKL$ , $KL=\sqrt{5}$ . Now continue with solution 1.

Solution 2

$[asy] size(10cm); pair A, B, C, D, H, K, O, P, L, M, X, Y; A = (-15, 27); B = (-24, 0); C = (24, 0); D = (-8.28, 18.04); O = (0, 7); P = (0, -7); H = (-15, 13); K = (-15, -13); M = (0, 0); L = (-15, 0); X = (-24.9569, 5.53234); Y = (8.39688, 30.5477); draw(circle(O, 25)); draw(circle(P, 25)); draw(A--B--C--cycle); draw(H -- K); draw(A -- O -- P -- H -- cycle); draw(X -- Y); draw(O -- X, dashed); draw(O -- Y, dashed); draw(O -- B, dashed); draw(O -- C, dashed); label("$O$", O, ENE); label("$A$", A, NW); label("$B$", B, W); label("$C$", C, E); label("$H$", H, E); label("$H'$", K, NE); label("$X$", X, W); label("$Y$", Y, NE); label("$O'$", P, E); label("$M$", M, NE); label("$L$", L, NE); label("$D$", D, NNE); label("$2$", X -- H, NW); label("$3$", H -- A, SW); label("$6$", H -- Y, NW); label("$R$", O -- Y, E); dot(O); dot(P); dot(D); dot(H); [/asy]$ Diagram not to scale.

We first observe that $H'$ , the image of the reflection of $H$ over line $BC$ , lies on circle $O$ . This is because $\angle HBC = 90 - \angle C = \angle H'AC = \angle H'BC$ . This is a well known lemma. The result of this observation is that circle $O'$ , the circumcircle of $\triangle BHC$ is the image of circle $O$ over line $BC$ , which in turn implies that $\overline{AH} = \overline{OO'}$ and thus $AHO'O$ is a parallelogram. That $AHO'O$ is a parallelogram implies that $AO$ is perpendicular to $\overline{XY}$ , and thus divides segment $\overline{XY}$ in two equal pieces, $\overline{XD}$ and $\overline{DY}$ , of length $4$ .

Using Power of a Point, $\overline{AH} \cdot \overline{HH'} = \overline{XH} \cdot \overline{HY} \Longrightarrow 3 \cdot \overline{HH'} = 2 \cdot 6 \Longrightarrow \overline{HH'} = 4$ This means that $\overline{HL} = \frac12 \cdot 4 = 2$ and $\overline{AL} = 2 + 3 = 5$ , where $L$ is the foot of the altitude from $A$ onto $BC$ . All that remains to be found is the length of segment $\overline{BC}$ .

Looking at right triangle $\triangle AHD$ , we find that $\overline{AD} = \sqrt{\overline{AH}^2 - \overline{HD}^2} = \sqrt{3^2 - 2^2} = \sqrt{5}$ Looking at right triangle $\triangle ODY$ , we get the equation $\overline{OY}^2 - \overline{DY}^2 = \overline{OD}^2 = \left(\overline{AO} - \overline{AD}\right)^2$ Plugging in known values, and letting $R$ be the radius of the circle, we find that $R^2 - 16 = (R - \sqrt{5})^2 = R^2 - 2\sqrt5 R + 5 \Longrightarrow R = \frac{21\sqrt5}{10}$

Recall that $AHO'O$ is a parallelogram, so $\overline{AH} = \overline{OO'} = 3$ . So, $\overline{OM} = \frac32$ , where $M$ is the midpoint of $\overline{BC}$ . This means that $\overline{BC} = 2\overline{BM} = 2\sqrt{R^2 - \left(\frac32\right)^2} = 2\sqrt{\frac{441}{20} - \frac{9}{4}} = \frac{6\sqrt{55}}{5}$

Thus, the area of triangle $\triangle ABC$ is $\frac{\overline{AL} \cdot \overline{BC}}{2} = \frac{5 \cdot \frac{6\sqrt{55}}{5}}{2} = {3\sqrt{55}}$ The answer is $3 + 55 = \boxed{058}$ .

Solution 3 (Official MAA 1)

Extend $\overline{AH}$ to intersect $\omega$ again at $P$ . The Power of a Point Theorem yields $HP = \tfrac{HX \cdot HY}{HA} = 4$ . Because $\angle CAP=\angle CBP$ , and $\angle CAP$ and $\angle CBH$ are both complements to $\angle C$ , it follows that $\angle CBP = \angle CBH$ , implying that $\overline{BC}$ bisects $\overline{HP}$ , so the length of the altitude from $A$ to $\overline{BC}$ is $h_a = AH + \tfrac12 HP = 5$ .

Let the circumcircle of $\triangle BCH$ be $\omega'$ . Because $\triangle BCH \cong \triangle BCP$ , the two triangles must have the same circumradius. Because the circumcircle of $\triangle BCP$ is $\omega$ , the circles $\omega$ and $\omega'$ have the same radius $R$ . Denote the centers of $\omega$ and $\omega'$ by $O$ and $O'$ , respectively, and let $M$ be the midpoint of $\overline{XY}$ . Note that trapezoid $HMOO'$ has $\angle H = \angle M = 90^\circ$ . Also $HM = XM - XH = \frac12\cdot XY - HX = 2$ and $HO' = R$ . Because $\omega$ is a translation of $\omega'$ in the direction of $\overline{AH}$ , it follows that $OO' = AH = 3$ . Finally, the Pythagorean Theorem applied to $\triangle XMO$ yields $MO = \sqrt{R^2-16}$ . Let $T$ be the projection of $O$ onto $\overline{HO'}$ . Then $TO' = R-MO$ , so the Pythagorean Theorem applied to $\triangle TOO'$ yields $R - \sqrt{R^2-16} = \sqrt{3^2 - 2^2} = \sqrt{5}.$ Solving for $R$ gives $R = \tfrac{21}{2\sqrt5}$ . It follows from properties of the orthocenter $H$ that $\cos\angle A = \dfrac{AH}{2R} = \dfrac{\sqrt5}{7},$ so $\sin\angle A = \sqrt{1 - \cos^2\angle A} = \dfrac{2\sqrt{11}}{7}.$ Therefore by the Extended Law of Sines $a = BC = 2R \sin\angle A = \dfrac{6\sqrt{11}}{\sqrt5},$ so $[\triangle ABC] = \frac12 a h_a = \frac12 \cdot \frac{6\sqrt{11}}{\sqrt{5}} \cdot 5 = 3\sqrt{55}.$ The requested sum is $3+55 = 58$ .

$[asy] unitsize(0.6 cm); pair A, B, C, D, H, M, O, Op, P, T, X, Y, Z; real R = 21/(2*sqrt(5)); A = (7/sqrt(5),7/2); O = (0,0); B = intersectionpoint((0,-3/2)--(R,-3/2),Circle(O,R)); C = intersectionpoint((0,-3/2)--(-R,-3/2),Circle(O,R)); H = A + B + C; P = reflect(B,C)*(H); D = (H + P)/2; Op = reflect(B,C)*(O); X = intersectionpoint(H--(H + scale(2)*rotate(90)*(Op - H)), Circle(O,R)); Y = intersectionpoint(H--(H + scale(2)*rotate(90)*(H - Op)), Circle(O,R)); Z = extension(X, Y, B, C); M = (X + Y)/2; T = H + O - M; draw(Circle(O,R)); draw(Circle(Op,R)); draw(A--B--C--cycle); draw(A--P); draw(B--Z--Y); draw(H--Op--O--M); draw(O--T); draw(O--X); dot("$A$", A, NE); dot("$B$", B, SW); dot("$C$", C, W); dot("$D$", D, SW); dot("$H$", H, NE); dot("$M$", M, NE); dot("$O$", O, W); dot("$O'$", Op, W); dot("$P$", P, SE); dot("$T$", T, N); dot("$X$", X, E); dot("$Y$", Y, NW); dot("$Z$", Z, E); label("$\omega$", R*dir(140), dir(140)); label("$\omega'$", Op + R*dir(220), dir(220)); [/asy]$

Solution 4 (Official MAA 2)

Let $D$ be the intersection point of line $AH$ and $\overline{BC}$ , noting that $\overline{AD}\perp\overline{BC}$ . Because the area of $\triangle ABC$ is $\tfrac12\cdot AD\cdot BC$ , it suffices to compute $AD$ and $BC$ separately. As in the previous solution, $AD = 5$ . The value of $BC$ can be found using the following lemma.

Lemma: Triangle $AXY$ is isosceles with base $\overline{XY}$ .

Proof: Because the circumcircle of $\triangle BCH$ , $\omega'$ , and $\omega$ have the same radius, there exists a translation $\Phi$ sending the former to the latter. Because $\overline{AH}$ is parallel to the line connecting the centers of the two circles, $\Phi$ must send $H$ to $A$ , meaning $\Phi$ also sends $\overline{XY}$ to the tangent to $\omega$ at $A$ . But this means that this tangent is parallel to $\overline{XY}$ , which implies the conclusion.

Applying Stewart's Theorem to $\triangle AXY$ yields $AX^2 = AH^2 + HX\cdot HY = 3^2 + 2\cdot 6 = 21,$ implying $AX = AY= \sqrt{21}.$

By the Law of Cosines $\cos \angle XAY = \frac{21 + 21 - 64}{2 \cdot 21} = -\frac{11}{21},$ so $\sin \angle XAY = \dfrac{4\sqrt{20}}{21}.$ Let $R$ be the radius of $\omega$ . By the Extended Law of Sines $R = \frac{XY}{2 \cdot \sin \angle XAY} = \dfrac{21}{\sqrt{20}}.$ Then the solution proceeds as in Solution 3.

Solution 5 (Official MAA 3)

Define points $D$ and $P$ as above, and note that $AD=5$ and $DH=PD=AD - AH = 2$ . Let the circumcircle of $\triangle BCH$ be $\omega'$ .

Extend $\overline{XY}$ past $X$ until it intersects line $BC$ at point $Z$ . Because line $BC$ is a radical axis of $\omega$ and $\omega'$ , it follows from the Power of a Point Theorem that $ZX \cdot ZY = ZX \cdot(ZX + 8) = ZH^2 = (ZX+2)^2,$ from which $ZX=1$ . By Pythagorean Theorem $ZD=\sqrt{ZH^2 - DH^2} = \sqrt{5}$ .

Let $m=CD$ and $n=BD$ . By the Power of a Point Theorem $mn= AD\cdot PD = 10.$ On the other hand, $ZH^2 = 9 = ZB \cdot ZC = (\sqrt{5} - n)(\sqrt{5} + m) = 5 + \sqrt{5}(m-n) - mn,$ from which $m-n = \frac{14}{\sqrt{5}}$ . Therefore

$(m+n)^2 = (m-n)^2 + 4mn = \frac{196}{5} + 40 = \frac{396}{5}.$ Thus $BC = m+n=\sqrt{\frac{396}{5}} = 6\sqrt{\frac{11}{5}}$ . Therefore $[\triangle ABC] = \frac{1}{2}BC \cdot AD = 3\sqrt{55},$ as above.

Video Solution

https://www.youtube.com/watch?v=L7B20E95s4M

Solution 6

Let $O$ be circumcenter of $ABC,$ let $R$ be circumradius of $ABC,$ let $\omega'$ be the image of circle $\omega$ over line $BC$ (the circumcircle of $HBC$ ).

Let $P$ be the image of the reflection of $H$ over line $BC, P$ lies on circle $\omega.$ Let $M$ be the midpoint of $XY.$ $P$ lies on $\omega,$ so $OA = OP = R,$ $OA = O'H, OA || O'H,$ so $M$ lies on $OA.$

https://brilliant.org/wiki/triangles-orthocenter/ or https://en.wikipedia.org/wiki/Altitude_(triangle) in russian language

We use properties of crossing chords and get $AH \cdot HP = XH \cdot HY = 2 \cdot 6 \implies HP = 4, AP = AH + HP = 7.$ We use properties of radius perpendicular chord and get $MH = \frac{XH + HY}{2} – HY = 2.$ We find $\sin OAH =\frac{MH}{AH} = \frac{2}{3} \implies \cos OAH = \frac{\sqrt{5}}{3}.$ We use properties of isosceles $\triangle OAP$ and find $R = \frac{AP}{2\cos OAP} = \frac{7}{2\frac {\sqrt{5}}{3}} = \frac{21}{2\sqrt{5}}.$ We use $OM' = \frac{AH}{2} = \frac {3}{2}$ and find $\frac{BC}{2} = \sqrt{R^2 – OM'^2} = 3 \sqrt {\frac {11}{5}}.$ The area of $ABC$ $\frac{BC}{2} \cdot (AH + HD) = 3\cdot \sqrt{55} \implies 3+55 = \boldsymbol{\boxed{058}}.$ ~vvsss, www.deoma-cmd.ru

2020 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 14	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search