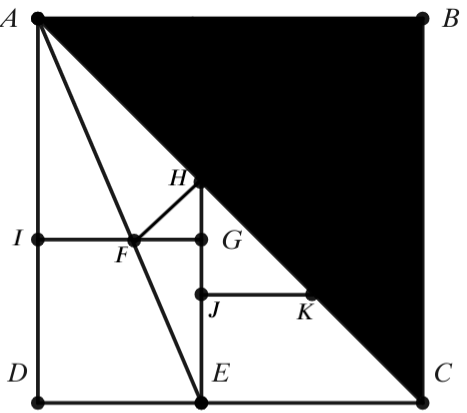
2021 April MIMC 10 Problems/Problem 22

In the diagram, $ABCD$ is a square with area $6+4\sqrt{2}$ . $AC$ is a diagonal of square $ABCD$ . Square $IGED$ has area $11-6\sqrt{2}$ . Given that point $J$ bisects line segment $HE$ , and $AE$ is a line segment. Extend $EG$ to meet diagonal $AC$ and mark the intersection point $H$ . In addition, $K$ is drawn so that $JK//EC$ . $FH^2$ can be represented as $\frac{a+b\sqrt{c}}{{d}}$ where $a,b,c,d$ are not necessarily distinct integers. Given that $gcd(a,b,d)=1$ , and $c$ does not have a perfect square factor. Find $a+b+c+d$ .

$\textbf{(A)} ~5 \qquad\textbf{(B)} ~15 \qquad\textbf{(C)} ~61 \qquad\textbf{(D)} ~349 \qquad\textbf{(E)} ~2009 \qquad$

Solution

To start this problem, we can first observe. Notice that $FGH$ is a right triangle because angle $FGH$ is supplementary to angle $IGE$ which is a right angle. Therefore, we just have to solve for the length of side $FG$ and $HG$ .

Solve for $FG$ : Triangles $AIF$ and $EGF$ are similar triangles, therefore, we can solve for length $AI$ . $AI=AD-ID$ . Use the technique of sum of squares and square root disintegration, $AD=2+\sqrt{2}$ . Using the same technique, $ID=3-\sqrt{2}$ . $AI=2+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}-1$ . Now, we can set up a ratio.

We can set $FG=x$ , so $IF=3-\sqrt{2}-x$ . Using the similar triangle, $\frac{GE}{AI}=\frac{FG}{IF}$ . Plugging the numbers into the ratio, we can get $\frac{3-\sqrt{2}}{2\sqrt{2}-1}=\frac{x}{3-\sqrt{2}-x}$ .

$~~~~~~~~~~~~~~~~~~~~~~\frac{3-\sqrt{2}}{2\sqrt{2}-1}=\frac{x}{3-\sqrt{2}-x}$

$~(3-\sqrt{2})(3-\sqrt{2}-x)=x(2\sqrt{2}-1)$

$11-6\sqrt{2}-(3-\sqrt{2})x=x(2\sqrt{2}-1)$

$~~~~~~~~~~~~~~~~~(2+\sqrt{2})x=11-6\sqrt{2}$

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x=\frac{11-6\sqrt{2}}{2+\sqrt{2}}$

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x=\frac{34-23\sqrt{2}}{2}$

Solve for $HG$ : Since angle $HEC$ is $90\degree$ (Error compiling LaTeX. Unknown error_msg) and angle $HCE$ is $45\degree$ (Error compiling LaTeX. Unknown error_msg), $EC=HE=2\sqrt{2}-1$ . Since $GE=3-\sqrt{2}$ , $HG=2\sqrt{2}-1-(3-\sqrt{2})=3\sqrt{2}-4$ . Finally, we can solve for $FH^2$ , that is, $FG^2+HG^2=(\frac{34-23\sqrt{2}}{2})^2+(3\sqrt{2}-4)^2=\frac{1175-830\sqrt{2}}{2}$ . Therefore, our answer would be $1175-830+2+2=\fbox{\textbf{(D)} 349}$ .

Page

Toolbox

Search

2021 April MIMC 10 Problems/Problem 22

Solution