2007 Cyprus MO/Lyceum/Problem 14
Problem
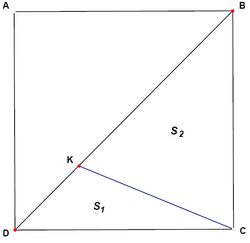
In square ![]() the segment
the segment ![]() equals a side of the square. The ratio of areas
equals a side of the square. The ratio of areas ![]() is
is
![]()
Solution
![]() and
and ![]() have the same heights (
have the same heights (![]() ), so the ratio of their areas is simply the ratio of
), so the ratio of their areas is simply the ratio of ![]() .
.
Let ![]() . Then
. Then ![]() , and the ratio of
, and the ratio of ![]() is
is ![]() , or
, or ![]() .
.
See also
| 2007 Cyprus MO, Lyceum (Problems) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||