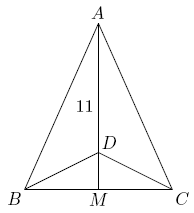
1995 AIME Problems/Problem 9
Problem
Triangle 
is isosceles, with 
and altitude 
Suppose that there is a point 
on 
with 
and 
Then the perimeter of 
may be written in the form 
where 
and 
are integers. Find 
Solution
Let 
, $\angleCDM=3x$ (Error compiling LaTeX. Unknown error_msg). Then, 
. Expanding tan 3x using the angle sum formula gives 
. Thus, 
. Solving, we get 
. Hence, 
and AC=
by Pythag. The total perimeter is double the sum of these, which is 
. The answer is then 
.
