1995 AIME Problems
Contents
Problem 1
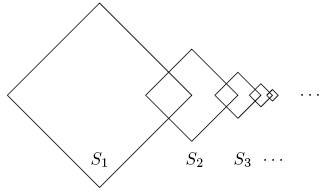
Square ![]() is
is ![]() For
For ![]() the lengths of the sides of square
the lengths of the sides of square ![]() are half the lengths of the sides of square
are half the lengths of the sides of square ![]() two adjacent sides of square
two adjacent sides of square ![]() are perpendicular bisectors of two adjacent sides of square
are perpendicular bisectors of two adjacent sides of square ![]() and the other two sides of square
and the other two sides of square ![]() are the perpendicular bisectors of two adjacent sides of square
are the perpendicular bisectors of two adjacent sides of square ![]() The total area enclosed by at least one of
The total area enclosed by at least one of ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 2
Find the last three digits of the product of the positive roots of
![]()
Problem 3
Starting at ![]() an object moves in the coordinate plane via a sequence of steps, each of length one. Each step is left, right, up, or down, all four equally likely. Let
an object moves in the coordinate plane via a sequence of steps, each of length one. Each step is left, right, up, or down, all four equally likely. Let ![]() be the probability that the object reaches
be the probability that the object reaches ![]() in six or fewer steps. Given that
in six or fewer steps. Given that ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are relatively prime positive integers, find
are relatively prime positive integers, find ![]()
Problem 4
Circles of radius ![]() and
and ![]() are externally tangent to each other and are internally tangent to a circle of radius
are externally tangent to each other and are internally tangent to a circle of radius ![]() . The circle of radius
. The circle of radius ![]() has a chord that is a common external tangent of the other two circles. Find the square of the length of this chord.
has a chord that is a common external tangent of the other two circles. Find the square of the length of this chord.