Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2002 AMC 12B Problems/Problem 20"

(→‎Problem)
(→‎Solution)
Line 9: Line 9:
 
\qquad\mathrm{(E)}\ 32</math>
 
\qquad\mathrm{(E)}\ 32</math>
  
−
== Solution ==
+
== Solution ==  
 
[[Image:2002_12B_AMC-20.png]]
 
[[Image:2002_12B_AMC-20.png]]
  
Line 26: Line 26:
 
Alternatively, we could note that since we found <math>x^2 + y^2 = 169</math>, segment <math>MN=13</math>. Right triangles <math>\triangle MON</math> and <math>\triangle XOY</math> are similar by Leg-Leg with a ratio of <math>\frac{1}{2}</math>, so <math>XY=2(MN)=\boxed{\mathrm{(B)}\ 26}</math>
 
Alternatively, we could note that since we found <math>x^2 + y^2 = 169</math>, segment <math>MN=13</math>. Right triangles <math>\triangle MON</math> and <math>\triangle XOY</math> are similar by Leg-Leg with a ratio of <math>\frac{1}{2}</math>, so <math>XY=2(MN)=\boxed{\mathrm{(B)}\ 26}</math>
  
−
There is the solution, folks! Overall, this problem's topic is associated with the Pythagorean theorem. If you do not understand this solution, you should take a look at everything about Pythagorean theorem. Please contact us if there are any questions, concerns, or doubts upon this problem,  
+
There is the solution, folks! Overall, this problem's topic is associated with the Pythagorean theorem. If you do not understand this solution, you should take a look at everything about Pythagorean theorem ad triangles. Please contact us if there are any questions, concerns, or doubts about this problem, and we will take a closer look at our solution.
−
        Thank you.
+
      I hope you have a wonderful day!  Thank you.
  
 
== See also ==
 
== See also ==

Revision as of 14:24, 21 June 2018

The following problem is from both the 2002 AMC 12B #20 and 2002 AMC 10B #22, so both problems redirect to this page.

Problem

Let $\triangle XOY$ be a right-angled triangle with $m\angle XOY = 90^{\circ}$. Let $M$ and $N$ be the midpoints of legs $OX$ and $OY$, respectively. Given that $XN = 19$ and $YM = 22$, find $XY$.

$\mathrm{(A)}\ 24 \qquad\mathrm{(B)}\ 26 \qquad\mathrm{(C)}\ 28 \qquad\mathrm{(D)}\ 30 \qquad\mathrm{(E)}\ 32$

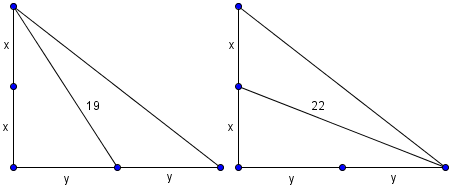
Solution

2002 12B AMC-20.png

Let $OM = x$, $ON = y$. By the Pythagorean Theorem on $\triangle XON, MOY$ respectively, \begin{align*} (2x)^2 + y^2 &= 19^2\\ x^2 + (2y)^2 &= 22^2\end{align*}

Summing these gives $5x^2 + 5y^2 = 845 \Longrightarrow x^2 + y^2 = 169$.

By the Pythagorean Theorem again, we have

\[(2x)^2 + (2y)^2 = XY^2 \Longrightarrow XY = \sqrt{4(x^2 + y^2)} = \sqrt{4(169)} = \sqrt{676} = \boxed{\mathrm{(B)}\ 26}\]

Alternatively, we could note that since we found $x^2 + y^2 = 169$, segment $MN=13$. Right triangles $\triangle MON$ and $\triangle XOY$ are similar by Leg-Leg with a ratio of $\frac{1}{2}$, so $XY=2(MN)=\boxed{\mathrm{(B)}\ 26}$

There is the solution, folks! Overall, this problem's topic is associated with the Pythagorean theorem. If you do not understand this solution, you should take a look at everything about Pythagorean theorem ad triangles. Please contact us if there are any questions, concerns, or doubts about this problem, and we will take a closer look at our solution. 

      I hope you have a wonderful day!  Thank you.

See also

2002 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2002 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2002_AMC_12B_Problems/Problem_20&oldid=95473"