Difference between revisions of "2006 AMC 10B Problems/Problem 24"

Revision as of 14:06, 2 August 2006

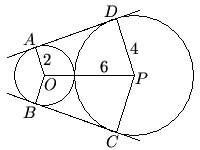
Problem

Circles with centers $O$ and $P$ have radii $2$ and $4$ , respectively, and are externally tangent. Points $A$ and $B$ on the circle with center $O$ and points $C$ and $D$ on the circle with center $P$ are such that $AD$ and $BC$ are common external tangents to the circles. What is the area of the concave hexagon $AOBCPD$ ?

$\mathrm{(A) \ } 18\sqrt{3}\qquad \mathrm{(B) \ } 24\sqrt{2}\qquad \mathrm{(C) \ } 36\qquad \mathrm{(D) \ } 24\sqrt{3}\qquad \mathrm{(E) \ } 32\sqrt{2}$

Solution

Since a tangent line is perpendicular to the radius containing the tangent point, $\angle OAD = \angle PDA = 90^\circ$ .

Construct a perpendicular to $DP$ that goes through point $O$ . Label the point of intersection $X$ .

Clearly $OADX$ is a rectangle.

Therefore $DX=2$ and $PX=2$ .

By the Pythagorean Theorem: $OX = \sqrt{6^2 - 2^2} = 4\sqrt{2}$ .

The area of $OADX$ is $2\cdot4\sqrt{2}=8\sqrt{2}$ .

The area of $OXP$ is $\frac{1}{2}\cdot2\cdot4\sqrt{2}=4\sqrt{2}$ .

So the area of quadrilateral $OADP$ is $8\sqrt{2}+4\sqrt{2}=12\sqrt{2}$ .

Using similar steps, the area of quadrilateral $OBCP$ is also $12\sqrt{2}$

Therefore, the area of hexagon $AOBCPD$ is $2\cdot12\sqrt{2}= 24\sqrt{2} \Rightarrow B$

@@ Line 29: / Line 29: @@
 == See Also ==
 *[[2006 AMC 10B Problems]]
+*[[2006 AMC 10B Problems/Problem 23|Previous Problem]]
+*[[2006 AMC 10B Problems/Problem 25|Next Problem]]

Page

Toolbox

Search

Difference between revisions of "2006 AMC 10B Problems/Problem 24"

Revision as of 14:06, 2 August 2006

Problem

Solution

See Also