Difference between revisions of "2003 USAMO Problems/Problem 4"
5849206328x (talk | contribs) (official solutions (rather, cleaning up solutions already present on page)) |
(→Solution 2) |
||
| Line 40: | Line 40: | ||
Combining the above, we conclude that <math>MF = MC</math> if and only if <math>MB\cdot MD = MC^2</math>. | Combining the above, we conclude that <math>MF = MC</math> if and only if <math>MB\cdot MD = MC^2</math>. | ||
| + | |||
| + | |||
| + | === Solution 3 === | ||
| + | We will construct a series of equivalent statements. First: | ||
| + | <cmath>\begin{align} | ||
| + | MB\cdot MD = MC^2 &\equiv \frac{MB}{MC} = \frac{MC}{MD} \\ | ||
| + | &\equiv \triangle MCD\sim \triangle MBC \\ | ||
| + | &\equiv \angle CBA = \angle FCA | ||
| + | \end{align}</cmath> | ||
| + | where the second equivalence follows from SAS similarity (because <math>\angle CMD = \angle BMC</math>). | ||
{{alternate solutions}} | {{alternate solutions}} | ||
Revision as of 22:06, 5 April 2016
Problem
Let ![]() be a triangle. A circle passing through
be a triangle. A circle passing through ![]() and
and ![]() intersects segments
intersects segments ![]() and
and ![]() at
at ![]() and
and ![]() , respectively. Lines
, respectively. Lines ![]() and
and ![]() intersect at
intersect at ![]() , while lines
, while lines ![]() and
and ![]() intersect at
intersect at ![]() . Prove that
. Prove that ![]() if and only if
if and only if ![]() .
.
Solutions
Solution 1
Extend segment ![]() through
through ![]() to
to ![]() such that
such that ![]() .
.
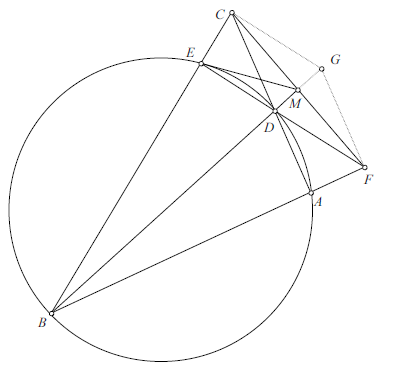
Then ![]() if and only if quadrilateral
if and only if quadrilateral ![]() is a parallelogram, or,
is a parallelogram, or, ![]() . Hence
. Hence ![]() if and only if
if and only if ![]() , that is,
, that is, ![]() .
.
Because quadrilateral ![]() is cyclic,
is cyclic, ![]() . It follows that
. It follows that ![]() if and only if
if and only if
![]() that is, quadrilateral
that is, quadrilateral ![]() is cyclic, which is equivalent to
is cyclic, which is equivalent to
![]() Because
Because ![]() ,
, ![]() if and only if triangles
if and only if triangles ![]() and
and ![]() are similar, that is
are similar, that is
![]() or
or ![]() .
.
Solution 2
We first assume that ![]() . Because
. Because ![]() and
and ![]() , triangles
, triangles ![]() and
and ![]() are similar. Consequently,
are similar. Consequently, ![]() .
.
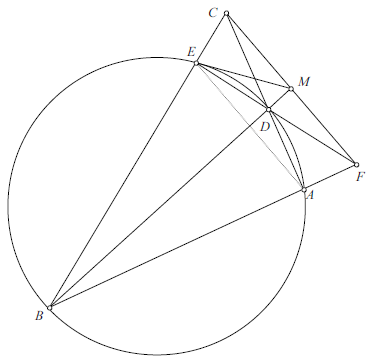
Because quadrilateral ![]() is cyclic,
is cyclic, ![]() . Hence
. Hence
![]() implying that
implying that ![]() , so
, so ![]() . Because quadrilateral
. Because quadrilateral ![]() is cyclic,
is cyclic, ![]() . Hence
. Hence
![]() Because
Because ![]() and
and ![]() , triangles
, triangles ![]() and
and ![]() are similar. Consequently,
are similar. Consequently, ![]() , or
, or ![]() . Therefore
. Therefore ![]() implies
implies ![]() .
.
Now we assume that ![]() . Applying Ceva's Theorem to triangle
. Applying Ceva's Theorem to triangle ![]() and cevians
and cevians ![]() gives
gives
![]() implying that
implying that ![]() , so
, so ![]() .
.
Consequently, ![]() . Because quadrilateral
. Because quadrilateral ![]() is cyclic,
is cyclic, ![]() . Hence
. Hence
![]() Because
Because ![]() and
and ![]() , triangles
, triangles ![]() and
and ![]() are similar. Consequently,
are similar. Consequently, ![]() , or
, or ![]() .
.
Combining the above, we conclude that ![]() if and only if
if and only if ![]() .
.
Solution 3
We will construct a series of equivalent statements. First:
 where the second equivalence follows from SAS similarity (because
where the second equivalence follows from SAS similarity (because ![]() ).
).
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See also
| 2003 USAMO (Problems • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









