Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 AIME A Problems/Problem 1"

(→‎Solution)
Line 25: Line 25:
 
<math>x=46</math>
 
<math>x=46</math>
  
−
Enter 046 in the answer circle.
+
The answer is therefore 046.
−
 
 
−
--[[User:Someperson01|Someperson01]] 21:27, 13 July 2006 (EDT)
 
  
 
== See also ==
 
== See also ==
 
*[[2006 AIME II Problems]]
 
*[[2006 AIME II Problems]]

Revision as of 16:35, 15 July 2006

Problem

In convex hexagon $ABCDEF$, all six sides are congruent, $\angle A$ and $\angle D$ are right angles, and $\angle B, \angle C, \angle D, \angle E,$ and $\angle F$ are congruent. The area of the hexagonal region is $2116(\sqrt{2}+1).$ Find $AB$.

Solution

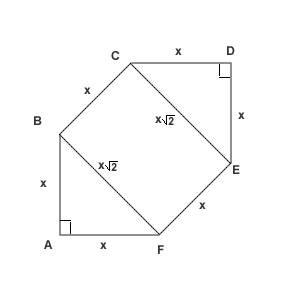
Let the side length be called $x$. Diagram1.png

Then $AB=BC=CD=DE=EF=AF=x$.

The diagonal $BF=\sqrt{AB^2+AF^2}=\sqrt{x^2+x^2}=x\sqrt{2}$.

Then the areas of the triangles AFB and CDE in total are $\frac{x^2}{2}\cdot 2$, and the area of the rectangle BCEF equals $x\cdot x\sqrt{2}=x^2\sqrt{2}$

Then we have to solve the equation

$2116(\sqrt{2}+1)=x^2\sqrt{2}+x^2$.

$2116(\sqrt{2}+1)=x^2(\sqrt{2}+1)$

$2116=x^2$

$x=46$

The answer is therefore 046.

See also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AIME_A_Problems/Problem_1&oldid=7729"