Difference between revisions of "2006 AIME A Problems/Problem 1"
Someperson01 (talk | contribs) (→Solution) |
|||
| Line 4: | Line 4: | ||
== Solution == | == Solution == | ||
| + | |||
| + | Let the side length be called <math>x</math>. | ||
| + | [[Image:Diagram1.png]] | ||
| + | |||
| + | Then <math>AB=BC=CD=DE=EF=AF=x</math>. | ||
| + | |||
| + | The diagonal <math>BF=\sqrt{AB^2+AF^2}=\sqrt{x^2+x^2}=x\sqrt{2}</math>. | ||
| + | |||
| + | Then the areas of the triangles AFB and CDE in total are <math>\frac{x^2}{2}\cdot 2</math>, | ||
| + | and the area of the rectangle BCEF equals <math>x\cdot x\sqrt{2}=x^2\sqrt{2}</math> | ||
| + | |||
| + | Then we have to solve the equation | ||
| + | |||
| + | <math>2116(\sqrt{2}+1)=x^2\sqrt{2}+x^2</math>. | ||
| + | |||
| + | <math>2116(\sqrt{2}+1)=x^2(\sqrt{2}+1)</math> | ||
| + | |||
| + | <math>2116=x^2</math> | ||
| + | |||
| + | <math>x=46</math> | ||
| + | |||
| + | Enter 046 in the answer circle. | ||
| + | |||
| + | --[[User:Someperson01|Someperson01]] 21:27, 13 July 2006 (EDT) | ||
== See also == | == See also == | ||
*[[2006 AIME II Problems]] | *[[2006 AIME II Problems]] | ||
Revision as of 20:27, 13 July 2006
Problem
In convex hexagon ![]() , all six sides are congruent,
, all six sides are congruent, ![]() and
and ![]() are right angles, and
are right angles, and ![]() and
and ![]() are congruent. The area of the hexagonal region is
are congruent. The area of the hexagonal region is ![]() Find
Find ![]() .
.
Solution
Let the side length be called ![]() .
.
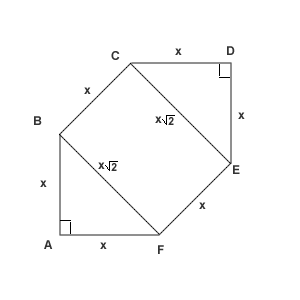
Then ![]() .
.
The diagonal ![]() .
.
Then the areas of the triangles AFB and CDE in total are ![]() ,
and the area of the rectangle BCEF equals
,
and the area of the rectangle BCEF equals ![]()
Then we have to solve the equation
![]() .
.
![]()
![]()
![]()
Enter 046 in the answer circle.
--Someperson01 21:27, 13 July 2006 (EDT)









