Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2003 AMC 10A Problems/Problem 22"

m (→‎Lemma)
(→‎Solution 4)
Line 101: Line 101:
 
=== Solution 4 ===
 
=== Solution 4 ===
 
We extend <math>BC</math> such that it intersects <math>GF</math> at <math>X</math>. Since <math>ABCD</math> is a rectangle, it follows that <math>CD=8</math>, therefore, <math>XF=8</math>. Let <math>GX=y</math>. From the similarity of triangles <math>GCH</math> and <math>GEA</math>, we have the ratio <math>3:5</math> (as <math>CH=9-6=3</math>, and <math>EA=9-4=5</math>). <math>GX</math> and <math>GF</math> are the altitudes of <math>GCH</math> and <math>GEA</math>, respectively. Thus, <math>y:y+8 = 3:5</math>, from which we have <math>y=12</math>, thus <math>GF=y+8=12+8=\boxed{\mathrm{(B)}\ 20}</math>
 
We extend <math>BC</math> such that it intersects <math>GF</math> at <math>X</math>. Since <math>ABCD</math> is a rectangle, it follows that <math>CD=8</math>, therefore, <math>XF=8</math>. Let <math>GX=y</math>. From the similarity of triangles <math>GCH</math> and <math>GEA</math>, we have the ratio <math>3:5</math> (as <math>CH=9-6=3</math>, and <math>EA=9-4=5</math>). <math>GX</math> and <math>GF</math> are the altitudes of <math>GCH</math> and <math>GEA</math>, respectively. Thus, <math>y:y+8 = 3:5</math>, from which we have <math>y=12</math>, thus <math>GF=y+8=12+8=\boxed{\mathrm{(B)}\ 20}</math>
 +
 +
== Solution 5 ==
 +
 +
Since <math>GF\perp AF</math> and <math>AF\perp CD, </math> we have <math>GF\parallel CD\parallel AB.</math> Thus, <math>\triangle CDE\sim GFE.</math> Suppose <math>GF=x</math> and <math>FD=y.</math> Thus, we have <math>\dfrac{x}{8}=\dfrac{y+4}{4}.</math> Additionally, now note that <math>\triangle GAF\sim AHB,</math> which is pretty obvious from insight, but can be proven by AA with extending <math>BH</math> to meet <math>GF.</math> From this new pair of similar triangles, we have <math>\dfrac{x}{8}=\dfrac{y+9}{6}.</math> Therefore, we have by combining those two equations, <cmath>\dfrac{y+9}{6}=\dfrac{y+4}{4}.</cmath> Solving, we have <math>y=6,</math> and therefore <math>x=\boxed{\mathrm{(B)}\ 20}</math>
  
 
== See Also ==
 
== See Also ==

Revision as of 17:34, 11 December 2015

Problem

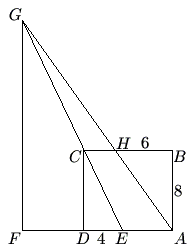
In rectangle $ABCD$, we have $AB=8$, $BC=9$, $H$ is on $BC$ with $BH=6$, $E$ is on $AD$ with $DE=4$, line $EC$ intersects line $AH$ at $G$, and $F$ is on line $AD$ with $GF \perp AF$. Find the length of $GF$.

2003amc10a22.gif

$\mathrm{(A) \ } 16\qquad \mathrm{(B) \ } 20\qquad \mathrm{(C) \ } 24\qquad \mathrm{(D) \ } 28\qquad \mathrm{(E) \ } 30$

Solution

Solution 1

$\angle GHC = \angle AHB$ (Opposite angles are equal).

$\angle F = \angle B$ (Both are 90 degrees).

$\angle BHA = \angle HAD$ (Alt. Interior Angles are congruent).

Therefore $\triangle GFA$ and $\triangle ABH$ are similar. $\triangle GCH$ and $\triangle GEA$ are also similar.

$DA$ is 9, therefore $EA$ must equal 5. Similarly, $CH$ must equal 3.

Because $GCH$ and $GEA$ are similar, the ratio of $CH\; =\; 3$ and $EA\; =\; 5$, must also hold true for $GH$ and $HA$. $\frac{GH}{GA} = \frac{3}{5}$, so $HA$ is $\frac{2}{5}$ of $GA$. By Pythagorean theorem, $(HA)^2\; =\; (HB)^2\; +\; (BA)^2\;...\;HA=10$.

$HA\: =\: 10 =\: \frac{2}{5}*(GA)$.

$GA\: =\: 25.$

So $\frac{GA}{HA}\: =\: \frac{GF}{BA}$.

$\frac{25}{10}\: =\: \frac{GF}{8}$.

Therefore $GF= \boxed{\mathrm{(B)}\ 20}$.

Solution 2

Since $ABCD$ is a rectangle, $CD=AB=8$.

Since $ABCD$ is a rectangle and $GF \perp AF$, $\angle GFE = \angle CDE = \angle ABC = 90^\circ$.

Since $ABCD$ is a rectangle, $AD || BC$.

So, $AH$ is a transversal, and $\angle GAF = \angle AHB$.

This is sufficient to prove that $GFE \approx CDE$ and $GFA \approx ABH$.

Using ratios:

$\frac{GF}{FE}=\frac{CD}{DE}$

$\frac{GF}{FD+4}=\frac{8}{4}=2$

$GF=2 \cdot (FD+4)=2 \cdot FD+8$

$\frac{GF}{FA}=\frac{AB}{BH}$

$\frac{GF}{FD+9}=\frac{8}{6}=\frac{4}{3}$

$GF=\frac{4}{3} \cdot (FD+9)=\frac{4}{3} \cdot FD+12$

Since $GF$ can't have 2 different lengths, both expressions for $GF$ must be equal.

$2 \cdot FD+8=\frac{4}{3} \cdot FD+12$

$\frac{2}{3} \cdot FD=4$

$FD=6$

$GF=2 \cdot FD+8=2\cdot6+8=\boxed{\mathrm{(B)}\ 20}$

Solution 3

Since $ABCD$ is a rectangle, $CH=3$, $EA=5$, and $CD=8$. From the Pythagorean Theorem, $CE^2=CD^2+DE^2=80\Rightarrow CE=4\sqrt{5}$.

Lemma

Statement: $GCH \approx GEA$

Proof: $\angle CGH=\angle EGA$, obviously.

\begin{eqnarray*} \angle HCE&=&180^{\circ}-\angle CHG\\ \angle DCE&=&\angle CHG-90^{\circ}\\ \angle CEED&=&180-\angle CHG\\ \angle GEA&=&\angle GCH \end{eqnarray*}

Since two angles of the triangles are equal, the third angles must equal each other. Therefore, the triangles are similar.


Let $GC=x$.

\begin{eqnarray*} \dfrac{x}{3}&=&\dfrac{x+4\sqrt{5}}{5}\\ 5x&=&3x+12\sqrt{5}\\ 2x&=&12\sqrt{5}\\ x&=&6\sqrt{5} \end{eqnarray*}

Also, $\triangle GFE\approx \triangle CDE$, therefore

\[\dfrac{8}{4\sqrt{5}}=\dfrac{GF}{10\sqrt{5}}\]

We can multiply both sides by $\sqrt{5}$ to get that $GF$ is twice of 10, or $\boxed{\mathrm{(B)}\ 20}$

Solution 4

We extend $BC$ such that it intersects $GF$ at $X$. Since $ABCD$ is a rectangle, it follows that $CD=8$, therefore, $XF=8$. Let $GX=y$. From the similarity of triangles $GCH$ and $GEA$, we have the ratio $3:5$ (as $CH=9-6=3$, and $EA=9-4=5$). $GX$ and $GF$ are the altitudes of $GCH$ and $GEA$, respectively. Thus, $y:y+8 = 3:5$, from which we have $y=12$, thus $GF=y+8=12+8=\boxed{\mathrm{(B)}\ 20}$

Solution 5

Since $GF\perp AF$ and $AF\perp CD,$ we have $GF\parallel CD\parallel AB.$ Thus, $\triangle CDE\sim GFE.$ Suppose $GF=x$ and $FD=y.$ Thus, we have $\dfrac{x}{8}=\dfrac{y+4}{4}.$ Additionally, now note that $\triangle GAF\sim AHB,$ which is pretty obvious from insight, but can be proven by AA with extending $BH$ to meet $GF.$ From this new pair of similar triangles, we have $\dfrac{x}{8}=\dfrac{y+9}{6}.$ Therefore, we have by combining those two equations, \[\dfrac{y+9}{6}=\dfrac{y+4}{4}.\] Solving, we have $y=6,$ and therefore $x=\boxed{\mathrm{(B)}\ 20}$

See Also

2003 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_10A_Problems/Problem_22&oldid=73608"