Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1992 AIME Problems/Problem 10"

(Undo revision 71027 by Starwars123 (talk))
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
 
Consider the region <math>A</math> in the complex plane that consists of all points <math>z</math> such that both <math>\frac{z}{40}</math> and <math>\frac{40}{\overline{z}}</math> have real and imaginary parts between <math>0</math> and <math>1</math>, inclusive. What is the integer that is nearest the area of <math>A</math>?
 
Consider the region <math>A</math> in the complex plane that consists of all points <math>z</math> such that both <math>\frac{z}{40}</math> and <math>\frac{40}{\overline{z}}</math> have real and imaginary parts between <math>0</math> and <math>1</math>, inclusive. What is the integer that is nearest the area of <math>A</math>?
−
<math>If  </math>z=a+bi<math> with </math>a<math> and </math>b<math> real, then </math>z=a-bi<math> is the conjugate of </math>z<math>)
 
  
 
== Solution ==
 
== Solution ==
−
Let </math>z=a+bi \implies \frac{z}{40}=\frac{a}{40}+\frac{b}{40}i<math>. Since </math>0\leq \frac{a}{40},\frac{b}{40}\leq 1<math> we have the inequality <cmath>0\leq a,b \leq 40</cmath>which is a square of side length </math>40<math>.
+
Let <math>z=a+bi \implies \frac{z}{40}=\frac{a}{40}+\frac{b}{40}i</math>. Since <math>0\leq \frac{a}{40},\frac{b}{40}\leq 1</math> we have the inequality <cmath>0\leq a,b \leq 40</cmath>which is a square of side length <math>40</math>.
  
−
Also, </math>\frac{40}{\overline{z}}=\frac{40}{a-bi}=\frac{40a}{a^2+b^2}+\frac{40b}{a^2+b^2}i<math> so we have </math>0\leq a,b \leq \frac{a^2+b^2}{40}<math>, which leads to:<cmath>(a-20)^2+b^2\geq 20^2</cmath>
+
Also, <math>\frac{40}{\overline{z}}=\frac{40}{a-bi}=\frac{40a}{a^2+b^2}+\frac{40b}{a^2+b^2}i</math> so we have <math>0\leq a,b \leq \frac{a^2+b^2}{40}</math>, which leads to:<cmath>(a-20)^2+b^2\geq 20^2</cmath>
 
<cmath>a^2+(b-20)^2\geq 20^2</cmath>
 
<cmath>a^2+(b-20)^2\geq 20^2</cmath>
  
Line 13: Line 12:
 
<center>[[Image:AIME_1992_Solution_10.png]]</center>
 
<center>[[Image:AIME_1992_Solution_10.png]]</center>
  
−
We want the area outside the two circles but inside the square. Doing a little geometry, the area of the intersection of those three graphs is </math>40^2-\frac{40^2}{4}-\frac{1}{2}\pi 20^2\approx 571.68<math>
+
We want the area outside the two circles but inside the square. Doing a little geometry, the area of the intersection of those three graphs is <math>40^2-\frac{40^2}{4}-\frac{1}{2}\pi 20^2\approx 571.68</math>
  
−
</math>\boxed{572}$
+
<math>\boxed{572}</math>
 +
== See also ==
 +
{{AIME box|year=1992|num-b=9|num-a=11}}
 +
 
 +
[[Category:Intermediate Algebra Problems]]
 +
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Revision as of 12:39, 8 July 2015

Problem

Consider the region $A$ in the complex plane that consists of all points $z$ such that both $\frac{z}{40}$ and $\frac{40}{\overline{z}}$ have real and imaginary parts between $0$ and $1$, inclusive. What is the integer that is nearest the area of $A$?

Solution

Let $z=a+bi \implies \frac{z}{40}=\frac{a}{40}+\frac{b}{40}i$. Since $0\leq \frac{a}{40},\frac{b}{40}\leq 1$ we have the inequality \[0\leq a,b \leq 40\]which is a square of side length $40$.

Also, $\frac{40}{\overline{z}}=\frac{40}{a-bi}=\frac{40a}{a^2+b^2}+\frac{40b}{a^2+b^2}i$ so we have $0\leq a,b \leq \frac{a^2+b^2}{40}$, which leads to:\[(a-20)^2+b^2\geq 20^2\] \[a^2+(b-20)^2\geq 20^2\]

We graph them:

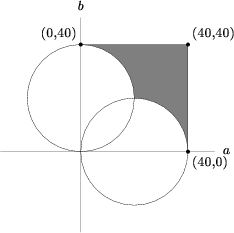
AIME 1992 Solution 10.png

We want the area outside the two circles but inside the square. Doing a little geometry, the area of the intersection of those three graphs is $40^2-\frac{40^2}{4}-\frac{1}{2}\pi 20^2\approx 571.68$

$\boxed{572}$

See also

1992 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 9 		Followed by
Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1992_AIME_Problems/Problem_10&oldid=71040"