Difference between revisions of "1983 AIME Problems/Problem 15"
(→Problem) |
|||
| Line 12: | Line 12: | ||
Next, notice that <math>\angle AOB = \angle AOM - \angle BOM</math>. We can therefore apply the tangent subtraction formula to obtain , <math>\tan AOB =\frac{\tan AOM - \tan BOM}{1 + \tan AOM \cdot \tan AOM} =\frac{\frac 4 3 - \frac 3 4}{1 + \frac 4 3 \cdot \frac 3 4} = \frac{7}{24}</math>. It follows that <math>\sin AOB =\frac{7}{\sqrt{7^2+24^2}} = \frac{7}{25}</math>, resulting in an answer of <math>7 \cdot 25=\boxed{175}</math>. | Next, notice that <math>\angle AOB = \angle AOM - \angle BOM</math>. We can therefore apply the tangent subtraction formula to obtain , <math>\tan AOB =\frac{\tan AOM - \tan BOM}{1 + \tan AOM \cdot \tan AOM} =\frac{\frac 4 3 - \frac 3 4}{1 + \frac 4 3 \cdot \frac 3 4} = \frac{7}{24}</math>. It follows that <math>\sin AOB =\frac{7}{\sqrt{7^2+24^2}} = \frac{7}{25}</math>, resulting in an answer of <math>7 \cdot 25=\boxed{175}</math>. | ||
| + | |||
| + | == Solution 2 == | ||
| + | <asy> | ||
| + | size(10cm); | ||
| + | import olympiad; | ||
| + | pair O = (0,0);dot(O);label("$O$",O,SW); | ||
| + | pair M = (4,0);dot(M);label("$M$",M,SE); | ||
| + | pair N = (4,2);dot(N);label("$N$",N,NE); | ||
| + | draw(circle(O,5)); | ||
| + | pair B = (4,3);dot(B);label("$B$",B,NE); | ||
| + | pair C = (4,-3);dot(C);label("$C$",C,SE); | ||
| + | draw(B--C);draw(O--M); | ||
| + | pair P = (1.5,2);dot(P);label("$P$",P,W); | ||
| + | draw(circle(P,2.5)); | ||
| + | pair A=(3,4);dot(A);label("$A$",A,NE); | ||
| + | draw(O--A); | ||
| + | draw(O--B); | ||
| + | pair Q = (1.5,0); dot(Q); label("$Q$",Q,S); | ||
| + | pair R = (3,0); dot(R); label("$R$",R,S); | ||
| + | draw(P--Q,dotted); draw(A--R,dotted); | ||
| + | pair D=(5,0); dot(D); label("$D$",D,E); | ||
| + | draw(A--D); | ||
| + | </asy> | ||
| + | |||
| + | The above solution works, but is quite messy and somewhat difficult to follow. This solution provides a diagram to scale, and the motivation behind the solution. | ||
| + | |||
| + | First of all, where did the statement "<math>AD</math> is the only chord starting at <math>A</math> and bisected by <math>BC</math> " come from? What is its significance in this problem? What is the criterion for this statement to be true? | ||
| + | |||
| + | We consider the locus of midpoints of the chords from <math>A</math>. It is well known that this is the circle with diameter <math>AO</math>, where <math>O</math> is the center of the circle. The proof is simple: every midpoint of a chord is a dilation of the endpoint with ratio <math>1/2</math> with center <math>A</math>. Thus, the locus is the result of the dilation with ratio <math>1/2</math> of circle <math>O</math> with center <math>A</math>. Let the center of this circle be <math>P</math>. | ||
| + | |||
| + | Aha! Now we see. <math>AD</math> is bisected by <math>BC</math> if they cross at some point <math>N</math> on the circle. Moreover, since <math>AD</math> is the only chord, <math>BC</math> must be tangent to the circle <math>P</math>. | ||
| + | |||
| + | The rest of this problem is straight forward. | ||
| + | |||
| + | Our goal is to find <math>\sin AOB = \sin (AOM - BOM)</math> where <math>M</math> is the midpoint of <math>BC</math>. Then we have <math>BM=3</math> and <math>OM=4</math>. | ||
| + | Let <math>R</math> be the projection of <math>A</math> onto <math>OM</math>, and similarly <math>Q</math> be the projection of <math>P</math> onto <math>OM</math>. Then it remains to find <math>AR</math> so we can use the sine addition formula. | ||
| + | |||
| + | As <math>PN</math> is a radius of circle <math>P</math>, <math>PN=2.5</math>, and similarly, <math>PO=2.5</math>. Since <math>OM=4</math>, <math>OQ=OM-QM=OM-PN=4-2.5=1.5</math>. Thus, <math>PQ=\sqrt{(2.5)^2-1.5^2}=2</math>. | ||
| + | |||
| + | From here, we see that <math>\triangle OAR</math> is a dilation of <math>\triangle OPQ</math> about center <math>O</math> with ratio <math>2</math>, so <math>AR=2PQ=4</math>. | ||
| + | |||
| + | Lastly, we apply the formula: | ||
| + | <cmath> \sin (AOM - BOM) = \sin AOM \cos BOM - \sin BOM \cos AOM = (4/5)(4/5)-(3/5)(3/5)=7/25.</cmath> | ||
| + | |||
| + | Thus, our answer is <math>7*25=\boxed{175}</math>. | ||
== See Also == | == See Also == | ||
Revision as of 01:18, 17 May 2015
Contents
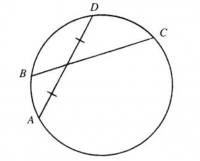
Problem
The adjoining figure shows two intersecting chords in a circle, with ![]() on minor arc
on minor arc ![]() . Suppose that the radius of the circle is
. Suppose that the radius of the circle is ![]() , that
, that ![]() , and that
, and that ![]() is bisected by
is bisected by ![]() . Suppose further that
. Suppose further that ![]() is the only chord starting at
is the only chord starting at ![]() which is bisected by
which is bisected by ![]() . It follows that the sine of the minor arc
. It follows that the sine of the minor arc ![]() is a rational number. If this fraction is expressed as a fraction
is a rational number. If this fraction is expressed as a fraction ![]() in lowest terms, what is the product
in lowest terms, what is the product ![]() ?
?
Solution
Let ![]() be any fixed point on circle
be any fixed point on circle ![]() and let
and let ![]() be a chord of circle
be a chord of circle ![]() . The locus of midpoints
. The locus of midpoints ![]() of the chord
of the chord ![]() is a circle
is a circle ![]() , with diameter
, with diameter ![]() . Generally, the circle
. Generally, the circle ![]() can intersect the chord
can intersect the chord ![]() at two points, one point, or they may not have a point of intersection. By the problem condition, however, the circle
at two points, one point, or they may not have a point of intersection. By the problem condition, however, the circle ![]() is tangent to BC at point N.
is tangent to BC at point N.
Let M be the midpoint of the chord ![]() . From right triangle
. From right triangle ![]() ,
, ![]() . Thus,
. Thus, ![]() .
.
Notice that the distance ![]() equals
equals ![]() (Where
(Where ![]() is the radius of circle P). Evaluating this,
is the radius of circle P). Evaluating this, ![]() . From
. From ![]() , we see that
, we see that ![]()
Next, notice that ![]() . We can therefore apply the tangent subtraction formula to obtain ,
. We can therefore apply the tangent subtraction formula to obtain , ![]() . It follows that
. It follows that ![]() , resulting in an answer of
, resulting in an answer of ![]() .
.
Solution 2
![[asy] size(10cm); import olympiad; pair O = (0,0);dot(O);label("$O$",O,SW); pair M = (4,0);dot(M);label("$M$",M,SE); pair N = (4,2);dot(N);label("$N$",N,NE); draw(circle(O,5)); pair B = (4,3);dot(B);label("$B$",B,NE); pair C = (4,-3);dot(C);label("$C$",C,SE); draw(B--C);draw(O--M); pair P = (1.5,2);dot(P);label("$P$",P,W); draw(circle(P,2.5)); pair A=(3,4);dot(A);label("$A$",A,NE); draw(O--A); draw(O--B); pair Q = (1.5,0); dot(Q); label("$Q$",Q,S); pair R = (3,0); dot(R); label("$R$",R,S); draw(P--Q,dotted); draw(A--R,dotted); pair D=(5,0); dot(D); label("$D$",D,E); draw(A--D); [/asy]](http://latex.artofproblemsolving.com/6/9/b/69b4209fd828eb0e7792dcfcf456596ec5e1a783.png)
The above solution works, but is quite messy and somewhat difficult to follow. This solution provides a diagram to scale, and the motivation behind the solution.
First of all, where did the statement "![]() is the only chord starting at
is the only chord starting at ![]() and bisected by
and bisected by ![]() " come from? What is its significance in this problem? What is the criterion for this statement to be true?
" come from? What is its significance in this problem? What is the criterion for this statement to be true?
We consider the locus of midpoints of the chords from ![]() . It is well known that this is the circle with diameter
. It is well known that this is the circle with diameter ![]() , where
, where ![]() is the center of the circle. The proof is simple: every midpoint of a chord is a dilation of the endpoint with ratio
is the center of the circle. The proof is simple: every midpoint of a chord is a dilation of the endpoint with ratio ![]() with center
with center ![]() . Thus, the locus is the result of the dilation with ratio
. Thus, the locus is the result of the dilation with ratio ![]() of circle
of circle ![]() with center
with center ![]() . Let the center of this circle be
. Let the center of this circle be ![]() .
.
Aha! Now we see. ![]() is bisected by
is bisected by ![]() if they cross at some point
if they cross at some point ![]() on the circle. Moreover, since
on the circle. Moreover, since ![]() is the only chord,
is the only chord, ![]() must be tangent to the circle
must be tangent to the circle ![]() .
.
The rest of this problem is straight forward.
Our goal is to find ![]() where
where ![]() is the midpoint of
is the midpoint of ![]() . Then we have
. Then we have ![]() and
and ![]() .
Let
.
Let ![]() be the projection of
be the projection of ![]() onto
onto ![]() , and similarly
, and similarly ![]() be the projection of
be the projection of ![]() onto
onto ![]() . Then it remains to find
. Then it remains to find ![]() so we can use the sine addition formula.
so we can use the sine addition formula.
As ![]() is a radius of circle
is a radius of circle ![]() ,
, ![]() , and similarly,
, and similarly, ![]() . Since
. Since ![]() ,
, ![]() . Thus,
. Thus, ![]() .
.
From here, we see that ![]() is a dilation of
is a dilation of ![]() about center
about center ![]() with ratio
with ratio ![]() , so
, so ![]() .
.
Lastly, we apply the formula:
![]()
Thus, our answer is ![]() .
.
See Also
| 1983 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||