Difference between revisions of "2004 AMC 12A Problems/Problem 18"
(→See also) |
m (→Solution 1) |
||
| Line 21: | Line 21: | ||
__TOC__ | __TOC__ | ||
==Solution== | ==Solution== | ||
| − | + | == Solution 1 == | |
| + | |||
<asy> | <asy> | ||
size(150); | size(150); | ||
| Line 49: | Line 50: | ||
x &= \frac{1}{2}\end{align*}</cmath> | x &= \frac{1}{2}\end{align*}</cmath> | ||
| − | Hence <math>CE = FC + x = \frac{5}{2} \Rightarrow \mathrm{(D)}</math>. | + | Hence <math>CE = FC + x = \frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}</math>. |
=== Solution 2 === | === Solution 2 === | ||
Revision as of 11:52, 21 July 2014
- The following problem is from both the 2004 AMC 12A #18 and 2004 AMC 10A #22, so both problems redirect to this page.
Problem
Square 
has side length 
. A semicircle with diameter 
is constructed inside the square, and the tangent to the semicircle from 
intersects side 
at 
. What is the length of 
?
![[asy] size(100); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2); draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180)); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); [/asy]](http://latex.artofproblemsolving.com/d/a/e/daef6f3ebe3e1fc6cfacd8611db1d6d449c8d2d4.png)
Solution
Solution 1
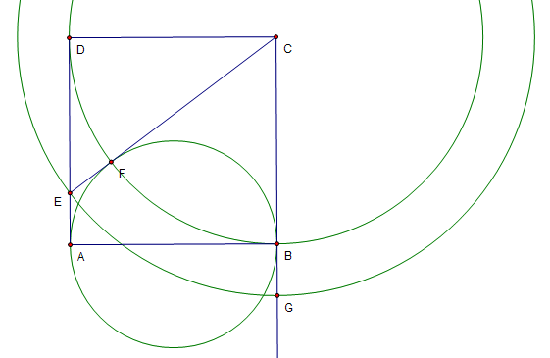
![[asy] size(150); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2), F=E+(C-E)/abs(C-E)/2; draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180));draw((A+B)/2--F); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); label("$F$",F,( 0, 1)); label("$x$",(A+E)/2,(-1, 0)); label("$x$",(E+F)/2,( 0, 1)); label("$2$",(F+C)/2,( 0, 1)); label("$2$",(D+C)/2,( 0, 1)); label("$2$",(B+C)/2,( 1, 0)); label("$2-x$",(D+E)/2,(-1, 0)); [/asy]](http://latex.artofproblemsolving.com/4/8/2/4820e9c378ef42e0fe36c7d37d2bb816d542a300.png)
Let the point of tangency be 
. By the Two Tangent Theorem 
and 
. Thus 
. The Pythagorean Theorem on 
yields
Hence 
.
Solution 2
Clearly, 
. Thus, the sides of right triangle 
are in arithmetic progression. Thus it is similar to the triangle 
and since 
, 
.
See also
| 2004 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 17 |
Followed by Problem 19 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
| 2004 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
