Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2003 USAMO Problems/Problem 4"

(→‎Solution 2)
(official solutions (rather, cleaning up solutions already present on page))
Line 3: Line 3:
 
Let <math>ABC</math> be a triangle. A circle passing through <math>A</math> and <math>B</math> intersects segments <math>AC</math> and <math>BC</math> at <math>D</math> and <math>E</math>, respectively. Lines <math>AB</math> and <math>DE</math> intersect at <math>F</math>, while lines <math>BD</math> and <math>CF</math> intersect at <math>M</math>. Prove that <math>MF = MC</math> if and only if <math>MB\cdot MD = MC^2</math>.
 
Let <math>ABC</math> be a triangle. A circle passing through <math>A</math> and <math>B</math> intersects segments <math>AC</math> and <math>BC</math> at <math>D</math> and <math>E</math>, respectively. Lines <math>AB</math> and <math>DE</math> intersect at <math>F</math>, while lines <math>BD</math> and <math>CF</math> intersect at <math>M</math>. Prove that <math>MF = MC</math> if and only if <math>MB\cdot MD = MC^2</math>.
  
−
== Solution ==
+
== Solutions ==
−
by April
+
=== Solution 1 ===
  
−
Take <math>G\in BD: \,FG\parallel CD</math>. We have:
+
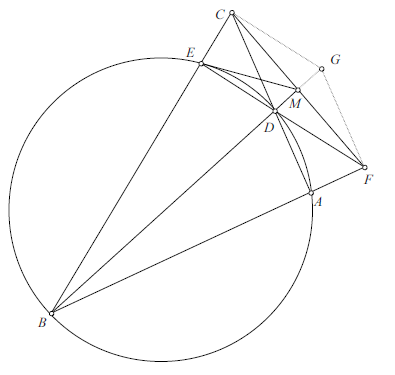
Extend segment <math>DM</math> through <math>M</math> to <math>G</math> such that <math>FG\parallel CD</math>.
  
−
<math>MF = MC\Longleftrightarrow \textrm{the quadrilateral}\; CDFG\; \textrm{is a parallelogram} \\
+
<center>[[File:2003usamo4-1.png]]</center>
−
\Longleftrightarrow FD\parallel CG\Longleftrightarrow\angle FDA = \angle GCD\Longleftrightarrow\angle FDA + \angle CGF = 180^\circ \\
 
−
\Longleftrightarrow \angle ABE + \angle CGF = 180^\circ\Longleftrightarrow\textrm{the quadrilateral}\;CBGF\;\textrm{is cyclic} \\
 
−
\Longleftrightarrow\angle CBM = \angle CBG = \angle CFG = \angle DCF = \angle DCM \\
 
−
\Longleftrightarrow\triangle BCM\sim\triangle CDM\Longleftrightarrow MB\cdot MD = MC^{2}</math>
 
  
−
Added diagram:
+
Then <math>MF = MC</math> if and only if quadrilateral <math>CDFG</math> is a parallelogram, or, <math>FD\parallel CG</math>. Hence <math>MC = MF</math> if and only if <math>\angle GCD = \angle FDA</math>, that is, <math>\angle FDA + \angle CGF = 180^\circ</math>.
  
−
<asy>
+
Because quadrilateral <math>ABED</math> is cyclic, <math>\angle FDA = \angle ABE</math>. It follows that <math>MC = MF</math> if and only if
−
import graph; size(5cm);
+
<cmath>180^\circ = \angle FDA + \angle CGF = \angle ABE + \angle CGF,</cmath>
−
real labelscalefactor = 0.5;
+
that is, quadrilateral <math>CBFG</math> is cyclic, which is equivalent to
−
pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); 
+
<cmath>\angle CBM = \angle CBG = \angle CFG = \angle DCF = \angle DCM.</cmath>
−
pen dotstyle = black; 
+
Because <math>\angle DMC = \angle CMB</math>, <math>\angle CBM = \angle DCM</math> if and only if triangles <math>BCM</math> and <math>CDM</math> are similar, that is
−
real xmin = -4.3, xmax = 6.36, ymin = -3.98, ymax = 6.3; 
+
<cmath>\frac{CM}{BM} = \frac{DM}{CM},</cmath>
−
draw((-0.16,3.1)--(-2.48,0.52));
+
or <math>MB\cdot MD = MC^2</math>.
−
draw((-2.48,0.52)--(3.78,0.52));
 
−
draw((3.78,0.52)--(-0.16,3.1));
 
−
draw(circle((-0.42,1), 2.12));
 
−
draw((1.04,4.43)--(3.78,0.52));
 
−
draw((1.04,4.43)--(-2.48,0.52));
 
−
draw((1.04,4.43)--(1.64,0.52));
 
−
draw((2.41,2.48)--(-2.48,0.52));
 
−
dot((-0.16,3.1),dotstyle);
 
−
label("$A$", (-0.4,3.3), NE * labelscalefactor);
 
−
dot((-2.48,0.52),dotstyle);
 
−
label("$B$", (-2.84,0.54), SW * labelscalefactor);
 
−
dot((3.78,0.52),dotstyle);
 
−
label("$C$", (3.86,0.64), NE * labelscalefactor);
 
−
dot((1.4,2.08),dotstyle);
 
−
label("$D$", (1.48,2.2), NE * labelscalefactor);
 
−
dot((1.64,0.52),dotstyle);
 
−
label("$E$", (1.72,0.64), NE * labelscalefactor);
 
−
dot((1.04,4.43),dotstyle);
 
−
label("$F$", (1.12,4.56), NE * labelscalefactor);
 
−
dot((2.41,2.48),dotstyle);
 
−
label("$M$", (2.48,2.6), NE * labelscalefactor);
 
−
clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle);
 
−
</asy>
 
  
−
==Solution 2==
+
=== Solution 2 ===
−
by suli
+
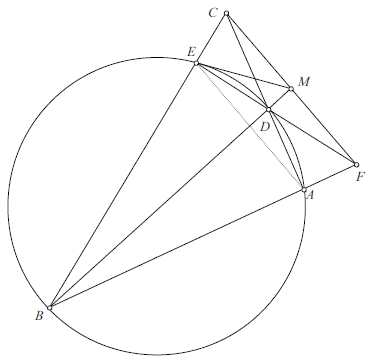
We first assume that <math>MB\cdot MD = MC^2</math>. Because <math>\frac{MC}{MD} = \frac{MB}{MC}</math> and <math>\angle CMD = \angle BMC</math>, triangles <math>CMD</math> and <math>BMC</math> are similar. Consequently, <math>\angle MCD = \angle MBC</math>.
  
−
Let's prove the first direction: if <math>MD * MB = MC^2</math>, then MF = MC.
+
<center>[[File:2003usamo4-2.png]]</center>
  
−
We start that noticing by SAS Similarity triangles MDC and MCB are similar. Thus, <MBC = <MCD. Because they intercept the same arc, <EAD = <MBC = <MCD and so EA // CF. It can further be shown that AF / AB = EC / EB using similar triangles. Now, let us use Ceva's Theorem on FBC to deduce that MF / MC = 1, and so MF = MC.
+
Because quadrilateral <math>ABED</math> is cyclic, <math>\angle DAE = \angle DBE</math>. Hence
 +
<cmath>\angle FCA = \angle MCD = \angle MBC = \angle DBE = \angle DAE = \angle CAE,</cmath>
 +
implying that <math>AE\parallel CF</math>, so <math>\angle AEF = \angle CFE</math>. Because quadrilateral <math>ABED</math> is cyclic, <math>\angle ABD = \angle AED</math>. Hence
 +
<cmath>\angle FBM = \angle ABD = \angle AED = \angle AEF = \angle CFE = \angle MFD.</cmath>
 +
Because <math>\angle FBM = \angle DFM</math> and <math>\angle FMB = \angle DMF</math>, triangles <math>BFM</math> and <math>FDM</math> are similar. Consequently, <math>\frac{FM}{DM} = \frac{BM}{FM}</math>, or <math>FM^2 = BM\cdot DM = CM^2</math>. Therefore <math>MC^2 = MB\cdot MD</math> implies <math>MC = MF</math>.
  
−
The other direction follows similarly; the proof will be left as an exercise for the reader.
+
Now we assume that <math>MC = MF</math>. Applying Ceva's Theorem to triangle <math>BCF</math> and cevians <math>BM, CA, FE</math> gives
 +
<cmath>\frac{BA}{AF}\cdot\frac{FM}{MC}\cdot\frac{CE}{EB} = 1,</cmath>
 +
implying that <math>\frac{BA}{AF} = \frac{BE}{EC}</math>, so <math>AE\parallel CF</math>.
 +
 
 +
Consequently, <math>\angle DCM = \angle DAE</math>. Because quadrilateral <math>ABED</math> is cyclic, <math>\angle DAE = \angle DBE</math>. Hence
 +
<cmath>\angle DCM = \angle DAE = \angle DBE = \angle CBM.</cmath>
 +
Because <math>\angle CBM = \angle DCM</math> and <math>\angle CMB = \angle DMC</math>, triangles <math>BCM</math> and <math>CDM</math> are similar. Consequently, <math>\frac{CM}{DM} = \frac{BM}{CM}</math>, or <math>CM^2 = BM\cdot DM</math>.
 +
 
 +
Combining the above, we conclude that <math>MF = MC</math> if and only if <math>MB\cdot MD = MC^2</math>.
 +
 
 +
{{alternate solutions}}
  
 
== See also ==
 
== See also ==

Revision as of 11:28, 17 July 2014

Problem

Let $ABC$ be a triangle. A circle passing through $A$ and $B$ intersects segments $AC$ and $BC$ at $D$ and $E$, respectively. Lines $AB$ and $DE$ intersect at $F$, while lines $BD$ and $CF$ intersect at $M$. Prove that $MF = MC$ if and only if $MB\cdot MD = MC^2$.

Solutions

Solution 1

Extend segment $DM$ through $M$ to $G$ such that $FG\parallel CD$.

2003usamo4-1.png

Then $MF = MC$ if and only if quadrilateral $CDFG$ is a parallelogram, or, $FD\parallel CG$. Hence $MC = MF$ if and only if $\angle GCD = \angle FDA$, that is, $\angle FDA + \angle CGF = 180^\circ$.

Because quadrilateral $ABED$ is cyclic, $\angle FDA = \angle ABE$. It follows that $MC = MF$ if and only if \[180^\circ = \angle FDA + \angle CGF = \angle ABE + \angle CGF,\] that is, quadrilateral $CBFG$ is cyclic, which is equivalent to \[\angle CBM = \angle CBG = \angle CFG = \angle DCF = \angle DCM.\] Because $\angle DMC = \angle CMB$, $\angle CBM = \angle DCM$ if and only if triangles $BCM$ and $CDM$ are similar, that is \[\frac{CM}{BM} = \frac{DM}{CM},\] or $MB\cdot MD = MC^2$.

Solution 2

We first assume that $MB\cdot MD = MC^2$. Because $\frac{MC}{MD} = \frac{MB}{MC}$ and $\angle CMD = \angle BMC$, triangles $CMD$ and $BMC$ are similar. Consequently, $\angle MCD = \angle MBC$.

2003usamo4-2.png

Because quadrilateral $ABED$ is cyclic, $\angle DAE = \angle DBE$. Hence \[\angle FCA = \angle MCD = \angle MBC = \angle DBE = \angle DAE = \angle CAE,\] implying that $AE\parallel CF$, so $\angle AEF = \angle CFE$. Because quadrilateral $ABED$ is cyclic, $\angle ABD = \angle AED$. Hence \[\angle FBM = \angle ABD = \angle AED = \angle AEF = \angle CFE = \angle MFD.\] Because $\angle FBM = \angle DFM$ and $\angle FMB = \angle DMF$, triangles $BFM$ and $FDM$ are similar. Consequently, $\frac{FM}{DM} = \frac{BM}{FM}$, or $FM^2 = BM\cdot DM = CM^2$. Therefore $MC^2 = MB\cdot MD$ implies $MC = MF$.

Now we assume that $MC = MF$. Applying Ceva's Theorem to triangle $BCF$ and cevians $BM, CA, FE$ gives \[\frac{BA}{AF}\cdot\frac{FM}{MC}\cdot\frac{CE}{EB} = 1,\] implying that $\frac{BA}{AF} = \frac{BE}{EC}$, so $AE\parallel CF$.

Consequently, $\angle DCM = \angle DAE$. Because quadrilateral $ABED$ is cyclic, $\angle DAE = \angle DBE$. Hence \[\angle DCM = \angle DAE = \angle DBE = \angle CBM.\] Because $\angle CBM = \angle DCM$ and $\angle CMB = \angle DMC$, triangles $BCM$ and $CDM$ are similar. Consequently, $\frac{CM}{DM} = \frac{BM}{CM}$, or $CM^2 = BM\cdot DM$.

Combining the above, we conclude that $MF = MC$ if and only if $MB\cdot MD = MC^2$.

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

See also

2003 USAMO (Problems • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2003_USAMO_Problems/Problem_4&oldid=62534"