Difference between revisions of "1992 AIME Problems/Problem 10"

Revision as of 18:24, 4 July 2013

Problem

Consider the region $A$ in the complex plane that consists of all points $z$ such that both $\frac{z}{40}$ and $\frac{40}{\overline{z}}$ have real and imaginary parts between $0$ and $1$ , inclusive. What is the integer that is nearest the area of $A$ ?

Solution

Let $z=a+bi \implies \frac{z}{40}=\frac{a}{40}+\frac{b}{40}i$ . Since $0\leq \frac{a}{40},\frac{b}{40}\leq 1$ we have the inequality $0\leq a,b \leq 40$ which is a square of side length $40$ .

Also, $\frac{40}{\overline{z}}=\frac{40}{a-bi}=\frac{40a}{a^2+b^2}+\frac{40b}{a^2+b^2}i$ so we have $0\leq a,b \leq \frac{a^2+b^2}{40}$ , which leads to: $(a-20)^2+b^2\geq 20^2$ $a^2+(b-20)^2\geq 20^2$

We graph them:

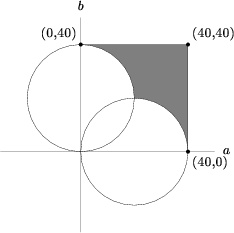
We want the area outside the two circles but inside the square. Doing a little geometry, the area of the intersection of those three graphs is $40^2-\frac{40^2}{4}-\frac{1}{2}\pi 20^2\approx 571.68$

$\boxed{572}$

@@ Line 20: / Line 20: @@
 [[Category:Intermediate Algebra Problems]]
 [[Category:Intermediate Geometry Problems]]
+{{MAA Notice}}

1992 AIME (Problems • Answer Key • Resources)
Preceded by Problem 9	Followed by Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

Difference between revisions of "1992 AIME Problems/Problem 10"

Revision as of 18:24, 4 July 2013

Problem

Solution

See also