Difference between revisions of "2002 AMC 12B Problems/Problem 20"
(soln) |
|||
| Line 24: | Line 24: | ||
== See also == | == See also == | ||
{{AMC12 box|year=2002|ab=B|num-b=19|num-a=21}} | {{AMC12 box|year=2002|ab=B|num-b=19|num-a=21}} | ||
| − | |||
| − | |||
Revision as of 01:13, 11 April 2009
Problem
Let 
be a right-angled triangle with 
. Let 
and 
be the midpoints of legs 
and 
, respectively. Given that 
and 
, find 
.
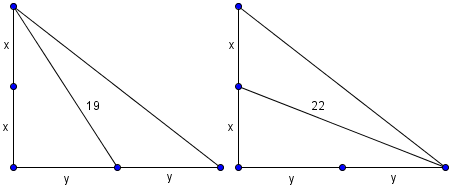
Solution
Let 
, 
. By the Pythagorean Theorem on 
respectively,
Summing these gives 
.
By the Pythagorean Theorem again, we have
![\[(2x)^2 + (2y)^2 = XY^2 \Longrightarrow XY = \sqrt{4(x^2 + y^2)} = 26 \Rightarrow \mathrm{(B)}\]](http://latex.artofproblemsolving.com/1/b/6/1b64d4fb2c2d9fcf5988a0a5317a988189690ca6.png)
See also
| 2002 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 19 |
Followed by Problem 21 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
