Difference between revisions of "Stewart's Theorem"

Latest revision as of 18:22, 18 February 2025

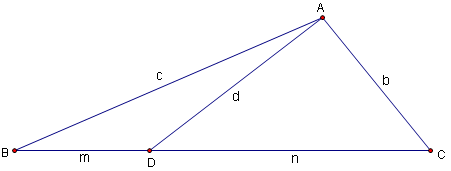
Statement

Given any triangle $\triangle ABC$ with sides of length $a, b, c$ and opposite vertices $A$ , $B$ , $C$ , respectively, then if cevian $AD$ is drawn so that $BD = m$ , $DC = n$ and $AD = d$ , we have that $b^2m + c^2n = amn + d^2a$ . (This is also often written $man + dad = bmb + cnc$ , a phrase which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink.") That is Stewart's Theorem.

Proof

Proof 1

Applying the Law of Cosines in triangle $\triangle ABD$ at angle $\angle ADB$ and in triangle $\triangle ACD$ at angle $\angle CDA$ , we get the following equations:

$n^{2} + d^{2} - 2nd\cos{\angle CDA} = b^{2}$
$m^{2} + d^{2} - 2md\cos{\angle ADB} = c^{2}$

Because angles $\angle ADB$ and $\angle CDA$ are supplementary, $m\angle ADB = 180^\circ - m\angle CDA$ . We can therefore solve both equations for the cosine term. Using the trigonometric identity $\cos{\theta} = -\cos{(180^\circ - \theta)}$ gives us

$\frac{n^2 + d^2 - b^2}{2nd} = \cos{\angle CDA}$
$\frac{c^2 - m^2 -d^2}{2md} = \cos{\angle CDA}$

Setting the two left-hand sides equal and clearing denominators, we arrive at the equation: $c^{2}n + b^{2}m=m^{2}n +n^{2}m + d^{2}m + d^{2}n$ . However, $m+n = a$ so $m^2n + n^2m = (m + n)mn = amn$ and $d^2m + d^2n = d^2(m + n) = d^2a.$ This simplifies our equation to yield $man + dad = bmb + cnc,$ as desired.

Proof 2 (Pythagorean Theorem)

Let the altitude from $A$ to $BC$ meet $BC$ at $H$ . Let $AH=h$ , $CH=x$ , and $HD=y$ .

We can apply the Pythagorean Theorem on $\triangle AHC$ and $\triangle AHD$ to yield

$h^2 = b^2 - x^2 = d^2 - y^2$ and then solve for b to get $b^2 = d^2 + x^2 - y^2$

Doing the same for $\triangle AHB$ and $\triangle AHD$

$h^2 = c^2 - (m + y)^2 = d^2 - y^2$ then solve for c to get $c^2 = d^2 + m^2 + 2my$

Now multiple the first expression by m and the second by n

$mb^2 = md^2 + m(x^2 - y^2)$ $nc^2 = nd^2 + m^2n + 2mny$

Next add these two expressions

$mb^2 + nc^2 = md^2 + m(x^2 - y^2) + nd^2 + m^2n + 2mny$ .

Then simplify as follows (we reapply x + y = n a few times while factoring):

$mb^2 + nc^2 = (m + n)d^2 + m(x+y)(x - y) + mn(n + 2y)$ $mb^2 + nc^2 = (m + n)d^2 + mn(x - y) + mn(n + 2y)$ $mb^2 + nc^2 = (m + n)d^2 + mn(x + y + n)$ $mb^2 + nc^2 = (m + n)d^2 + mn(m + n)$ $mb^2 + nc^2 = (m + n)(d^2 + mn)$

Rearranging the equation gives Stewart's Theorem:

$man+dad = bmb+cnc$

Proof 3 (Barycentrics)

Let the following points have the following coordinates:

$A: (1,0,0)$

$B: (0,1,0)$

$C: (0,0,1)$

$D: \left(0, \frac{n}{m+n},\frac{m}{m+n}\right)$

Our displacement vector $\overrightarrow{AD}$ has coordinates $\left(1, -\frac{n}{m+n}, -\frac{m}{m+n}\right)$ . Plugging this into the barycentric distance formula, we obtain $d^2=-(m+n)^2 \left(\frac{mn}{(m+n)^2} \right)-b^2 \left ( -\frac{m}{m+n} \right)-c^2 \left(-\frac{n}{m+n}\right)=-mn+\frac{b^2m+c^2n}{m+n}$ Multiplying by $m+n$ , we get $d^2(m+n)+mn(m+n)=b^2m+c^2n$ . Substituting $m+n$ with $a$ , we find Stewart's Theorem: $\boxed{d^2a+amn=b^2m+c^2n}$

Video Proof

TheBeautyofMath

@@ Line 26: / Line 26: @@
 We can apply the [[Pythagorean Theorem]] on <math>\triangle AHC</math> and <math>\triangle AHD</math> to yield
-<cmath>h^2 = b^2 - x^2 = d^2 - y^2<math>  and then solve for b to get  </math>b^2 = d^2 + x^2 - y^2</cmath>
+<math>h^2 = b^2 - x^2 = d^2 - y^2</math>  and then solve for b to get  <math>b^2 = d^2 + x^2 - y^2</math>
 Doing the same for <math>\triangle AHB</math> and <math>\triangle AHD</math>
-<cmath>h^2 = c^2 - (m + y)^2 = d^2 - y^2<math> then solve for c to get </math>c^2 = d^2 + m^2 + 2my</cmath>
+<math>h^2 = c^2 - (m + y)^2 = d^2 - y^2</math> then solve for c to get <math>c^2 = d^2 + m^2 + 2my</math>
 Now multiple the first expression by m and the second by n

Page

Toolbox

Search