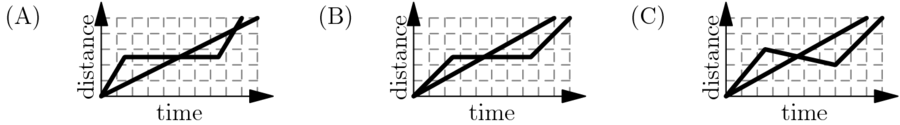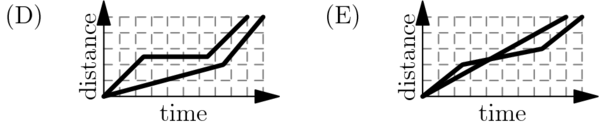Difference between revisions of "2019 AMC 8 Problems/Problem 5"
Roy1983zhang (talk | contribs) m (→Solution 1 - Using the answers) |
m (Formatting) |
||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| + | |||
A tortoise challenges a hare to a race. The hare eagerly agrees and quickly runs ahead, leaving the slow-moving tortoise behind. Confident that he will win, the hare stops to take a nap. Meanwhile, the tortoise walks at a slow steady pace for the entire race. The hare awakes and runs to the finish line, only to find the tortoise already there. Which of the following graphs matches the description of the race, showing the distance <math>d</math> traveled by the two animals over time <math>t</math> from start to finish? | A tortoise challenges a hare to a race. The hare eagerly agrees and quickly runs ahead, leaving the slow-moving tortoise behind. Confident that he will win, the hare stops to take a nap. Meanwhile, the tortoise walks at a slow steady pace for the entire race. The hare awakes and runs to the finish line, only to find the tortoise already there. Which of the following graphs matches the description of the race, showing the distance <math>d</math> traveled by the two animals over time <math>t</math> from start to finish? | ||
| Line 8: | Line 9: | ||
==Solutions== | ==Solutions== | ||
| + | ==Solution== | ||
| + | First, the tortoise walks at a constant rate, ruling out <math>(D)</math>. Second, when the hare is resting, the distance will stay the same, ruling out <math>(E)</math> and <math>(C)</math>. Third, the tortoise wins the race, meaning that the non-constant one should go off the graph last, ruling out <math>(A)</math>. The answer <math>\boxed{\textbf{(B)}}</math> is the only one left. | ||
| − | + | <!--Note to the original author of this solution: "we shouldn't be able to edit" is incorrect (if its definition is what I think it is), because I was able to edit. Also, I deleted that, (but did nothing else)--> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==Video Solution by Math-X (First fully understand the problem | + | ==Video Solution 1 by Math-X (First fully understand the problem)== |
https://youtu.be/IgpayYB48C4?si=zrQW67K2J_vVISHd&t=871 | https://youtu.be/IgpayYB48C4?si=zrQW67K2J_vVISHd&t=871 | ||
| − | + | ==Video Solution 2 (HOW TO THINK CREATIVELY)== | |
| − | |||
| − | ==Video Solution (HOW TO THINK CREATIVELY | ||
https://youtu.be/AH2uNkg67oo | https://youtu.be/AH2uNkg67oo | ||
~Education, the Study of Everything | ~Education, the Study of Everything | ||
| − | == Video Solution == | + | == Video Solution 3 == |
| − | + | https://youtu.be/IiFFDDITE6Q | |
| + | The Learning Royal | ||
| − | == Video Solution | + | == Video Solution 4 == |
| − | + | https://www.youtube.com/watch?v=uQTM8Kmh9B8&list=PLbhMrFqoXXwmwbk2CWeYOYPRbGtmdPUhL&index=6 | |
| − | ==Video Solution | + | ==Video Solution 5== |
https://youtu.be/FDG99LC75vA | https://youtu.be/FDG99LC75vA | ||
~savannahsolver | ~savannahsolver | ||
| − | ==Video Solution by The Power of Logic( | + | ==Video Solution 6 by The Power of Logic (Solutions to all problems)== |
https://youtu.be/Xm4ZGND9WoY | https://youtu.be/Xm4ZGND9WoY | ||
| Line 50: | Line 42: | ||
==See also== | ==See also== | ||
| + | |||
{{AMC8 box|year=2019|num-b=4|num-a=6}} | {{AMC8 box|year=2019|num-b=4|num-a=6}} | ||
| − | |||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 15:15, 18 January 2025
Contents
Problem
A tortoise challenges a hare to a race. The hare eagerly agrees and quickly runs ahead, leaving the slow-moving tortoise behind. Confident that he will win, the hare stops to take a nap. Meanwhile, the tortoise walks at a slow steady pace for the entire race. The hare awakes and runs to the finish line, only to find the tortoise already there. Which of the following graphs matches the description of the race, showing the distance 
traveled by the two animals over time 
from start to finish?
Solutions
Solution
First, the tortoise walks at a constant rate, ruling out 
. Second, when the hare is resting, the distance will stay the same, ruling out 
and 
. Third, the tortoise wins the race, meaning that the non-constant one should go off the graph last, ruling out 
. The answer 
is the only one left.
Video Solution 1 by Math-X (First fully understand the problem)
https://youtu.be/IgpayYB48C4?si=zrQW67K2J_vVISHd&t=871
Video Solution 2 (HOW TO THINK CREATIVELY)
~Education, the Study of Everything
Video Solution 3
https://youtu.be/IiFFDDITE6Q The Learning Royal
Video Solution 4
https://www.youtube.com/watch?v=uQTM8Kmh9B8&list=PLbhMrFqoXXwmwbk2CWeYOYPRbGtmdPUhL&index=6
Video Solution 5
~savannahsolver
Video Solution 6 by The Power of Logic (Solutions to all problems)
~Hayabusa1
See also
| 2019 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
