Difference between revisions of "2024 AIME II Problems/Problem 5"
(→Solution 1) |
Kempu33334 (talk | contribs) m (→Solution 1) |
||
| Line 7: | Line 7: | ||
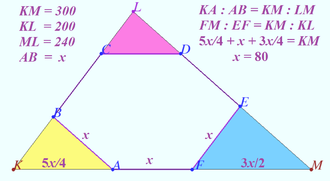
Let <math>AF \cap BC</math>, <math>BC \cap DE</math>, and <math>AF \cap DE</math> be K, L, and M, respectively. Let <math>KL=200, KM=300, ML=240</math>. | Let <math>AF \cap BC</math>, <math>BC \cap DE</math>, and <math>AF \cap DE</math> be K, L, and M, respectively. Let <math>KL=200, KM=300, ML=240</math>. | ||
| − | Notice that all smaller triangles formed are all similar to the larger <math>(200,240,300)</math> triangle. | + | Notice that because of the parallel condition, all smaller triangles formed are all similar to the larger <math>(200,240,300)</math> triangle. |
Let the side length of the hexagon be <math>x.</math> | Let the side length of the hexagon be <math>x.</math> | ||
Revision as of 13:28, 28 December 2024
Problem
Let ABCDEF be a convex equilateral hexagon in which all pairs of opposite sides are parallel. The triangle whose sides are extensions of segments AB, CD, and EF has side lengths 200, 240, and 300. Find the side length of the hexagon.
Solution 1
Draw a good diagram!
Let ![]() ,
, ![]() , and
, and ![]() be K, L, and M, respectively. Let
be K, L, and M, respectively. Let ![]() .
.
Notice that because of the parallel condition, all smaller triangles formed are all similar to the larger ![]() triangle.
triangle.
Let the side length of the hexagon be ![]()
Triangle ![]() , so
, so ![]() .
.
Triangle ![]() , so
, so ![]() .
.
We know ![]() , so
, so ![]() . Solving, we get
. Solving, we get ![]() .
.
-westwoodmonster
Solution 2 (Fakesolve)
Draw an accurate diagram using the allowed compass and ruler: Draw a to-scale diagram of the ![]() triangle (e.g. 10cm-12cm-15cm). Because of the nature of these lengths and the integer answer needed, it can be assumed that the side length of the hexagon will be divisible by 10. Therefore, a trial-and-error method can be set up, wherein line segments of length
triangle (e.g. 10cm-12cm-15cm). Because of the nature of these lengths and the integer answer needed, it can be assumed that the side length of the hexagon will be divisible by 10. Therefore, a trial-and-error method can be set up, wherein line segments of length ![]() , scaled to the same scale as the triangle, can be drawn to represent the sides of the hexagon. For instance, side
, scaled to the same scale as the triangle, can be drawn to represent the sides of the hexagon. For instance, side ![]() would be drawn parallel to the side of the triangle of length 300, and would have endpoints on the other sides of the triangle. Using this method, it would be evident that line segments of length 80 units, scaled proportionally (4cm using the scale above), would create a perfect equilateral hexagon when drawn parallel to the sides of the triangle.
would be drawn parallel to the side of the triangle of length 300, and would have endpoints on the other sides of the triangle. Using this method, it would be evident that line segments of length 80 units, scaled proportionally (4cm using the scale above), would create a perfect equilateral hexagon when drawn parallel to the sides of the triangle. ![]() . - lackolith
. - lackolith
Note
This problem is really similar to 2021 AMC 10 Problem 21. This really emphasizes the importance of studying up on past tests before taking the AMC.
-DoHumanitariansEatHumans
Video Solution
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
See also
| 2024 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()